<< 返回本书主页
<< Back to the afterword page

9 社会网络中的影响力与共识

吕汶桧 Wenhui Lyu

Jan. 2022

codes

9.1 背景问题

我们可以用有向图表示一个节点对其他节点的认同，有向边$i\to j$$i\to j$（$A[i,j]=1$$A[i,j]=1$）指的是，节点$i$$i$认同节点$j$$j$。

有向图的性质

方向性的存在意味着一系列新的性质：

	无向图	有向图
$n$$n$个节点的图的最大边数	${\displaystyle \frac{n(n-1)}{2}}$$\dfrac{n(n-1)}{2}$	$n(n-1)$$n(n-1)$
如果$A$$A$到$B$$B$的最短有向路径长度（距离）记为$AB$$AB$，$A$$A$到$C$$C$的最短有向路径长度记为$AC$$AC$，那么$B$$B$到$C$$C$的有向路径长度$BC\le AB+AC$$BC\leq AB+AC$	对	错

• 如果一个有穷有向图中不存在有向环，则该图中既存在出度为0的节点，也存在入度为0的节点；
• 如果有一个节点，它与其他每个节点分别都有两个方向的路径，则图中所有节点对之间都有两个方向的路径（即该图为强连通图）。

强连通图指的是满足如下条件的节点子集及其节点之间的边构成的子图$S$$S$：

1. $S$$S$中任何两个节点之间都有双向路径（长度可以大于1）；
2. $S$$S$之外不再有任何节点，既可以经$G$$G$中的有向路径到达$S$$S$，也可以从$S$$S$到达它。

若一个节点与任何其他节点都没有双向路径，则它自己构成一个强连通分量。

例如，下面这个有向图存在$7$$7$个强连通分量：

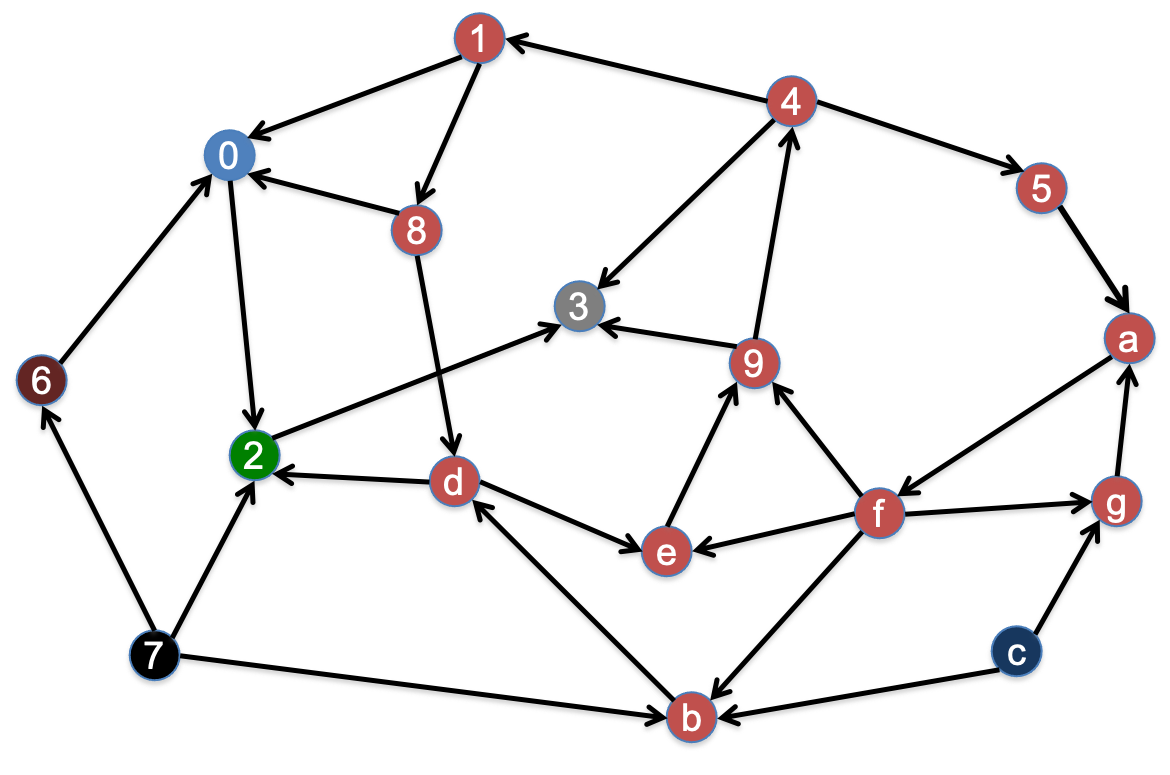
根据定义，可以通过广度优先搜索（BFS，见第三讲）找出有向图中的强连通分量：先用BFS找出节点$x$$x$沿出向边所能到达的节点集合为$F$$F$，再找出沿入向边能到达$x$$x$的节点集合为$B$$B$，则$F\cap B$$F\cap B$就是包含$x$$x$的强连通分量。

“重要性”评估：PageRank

有向边意味着“认同”关系，入度越高的节点，观点越受社会网络中的其他人重视，重要性越高。为了进一步利用有向图来评估每一节点的重要性，我们设置如下的操作化条件：

• 考虑整个“社会网络”有一个总价值，等于所有人的价值之和。（因为人和人之间，这种价值的绝对值意义不大，有意义的是相对值。）
• 让“被认可”（或“被推荐”）体现的价值与“推荐人”的价值成正比，同时与推荐人推荐的人数成反比。

由于不同节点的价值之间相互关联和影响（“被认可”体现的价值与“推荐人”的价值成正比），我们可以解方程来求解，也可以设每一节点的初始价值为$\frac{1}{n}$$\frac{1}{n}$（共$n$$n$个节点），然后迭代进行节点价值的更新：利用前一轮里每一节点的价值、根据他们的相互推荐，计算下一轮里每一节点的价值，再重复这一操作。迭代算法被搜索引擎用来确定网页的排序，故称为PageRank，具体地，这是PageRank的基本更新算法。

基本更新算法无法合理处理某些特殊情况。例如吸血鬼节点：一个节点总是只指向自己、只把认同价值分给自己，与此同时吸收其他节点的认同价值（下方左图的节点$x$$x$）；或者，少数几个节点互相认同、在内部瓜分认同价值；与此同时吸收其他节点的认同价值（下方右图的节点$x,y$$x,y$）。

克服这种挑战的措施就是在迭代过程的每一轮，都做“同比缩减，等量补偿”——类比按收入的统一百分比交税，然后发等量救济款。每个节点得以平等地保有一些价值，避免了网络中的认同价值被少数几个吸血鬼节点吸纳。用一个占比因子$s$$s$调控同比缩减的力度，$0<s<1$$0<s<1$，通常选在$0.85$$0.85$左右。

社会共识的形成：DeGroot Consensus

有向边意味着“认同”关系，如果节点$i$$i$认同$j$$j$，$j$$j$的态度和观点可能对$i$$i$有很大影响；因此，有向图中的“认同”网络还能用来模拟社会中观点之间的互相影响，这种互相影响可能导向社会共识。进一步的操作化算法如下：

1. 公开每个人的当前表态（认识）；
2. 每个人用自己认为靠谱的人的均值更新自己的表态；
3. 若稳定了就停止，否则回到 1。

9.2 计算实践：网络中影响力与共识的关系

codes

9.2.1 作业描述与算法思路

社会共识形成的算法迭代进行观点的更新。对于已稳定下来的情况，直观上我们会认为，社会共识与每个节点的影响力或PageRank有关系，共识应当接近影响力大的人的观点。

具体地，用向量$\overrightarrow{p}=(p_1,p_2,\dots ,p_n)$$\vec p=(p_1,p_2,\ldots,p_n)$表示每个节点的PageRank，用$\overrightarrow{s}=(s_1,s_2,\dots ,s_n)$$\vec s=(s_1,s_2,\ldots,s_n)$表示每个节点的观点初值，用数值$c$$c$表示DeGroot共识的结果。三者之间其实有如下关系

这一理论能在数学上得到证明。本次作业是在一个例子模型中编程验证这一理论：

• 输入一个合适的有向图邻接矩阵$A$$A$、一个认识初值向量$\overrightarrow{s}$$\vec s$；
• 程序首先根据$S$$S$，按照DeGroot模型得到共识值$c$$c$，再以节点初值$\frac{1}{n}$$\frac{1}{n}$算得采用基本更新算法下的PageRank向量$\overrightarrow{p}$$\vec p$；
• 验证$c=\overrightarrow{p}\cdot \overrightarrow{s}$$c=\vec p \cdot \vec s$的关系是否成立。

PageRank算法中价值的更新和DeGroot算法中观点的更新，都涉及矩阵向量乘法。以如下的认同有向图$A$$A$为例，

PageRank算法中更新节点价值时，由于一条认同边的价值与“推荐人”的推荐数成反比，我们要先对矩阵行做归一化，每一行总和值为$1$$1$。归一化后的值意味着，每个“推荐人”的推荐数越多，单个推荐的价值就越低。

第$i$$i$轮迭代中，每个节点有一当前价值，用向量${\overrightarrow{v}}_i=(v_1,v_2,\dots ,v_n)$$\vec v_i=(v_1,v_2,\ldots,v_n)$表示，初始值${\overrightarrow{v}}_0=(\underset{n\text{个}}{\underbrace{\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n}}})$$\vec v_0=(\underbrace{\frac{1}{n}, \frac{1}{n}, \ldots, \frac{1}{n}}_{n个})$。

把$\overrightarrow{v}$$\vec v$（推荐人的价值）与$A^{\ast }$$A^*$的列$i$$i$（推荐人的分量）做点乘，就可以得到节点$i$$i$的新价值。这意味着我们需要转置（转换行列）${\overrightarrow{v}}_i$$\vec v_i$和$A^{\ast }$$A^*$，再把二者做点乘就能得到新的PageRank ${\overrightarrow{v}}_{i+1}$$\vec v_{i+1}$：

在DeGroot算法中，每个节点更新自己的观点时，要把自己认同的人的观点做加权平均，这也意味着我们需要把矩阵$A$$A$标准化为$A^{\ast }$$A^*$，这一步同$(1)\to (2)$$(1)\to(2)$。标准化后的值意味着，认可$k$$k$个人的节点$i$$i$，其中一个被认同者$j$$j$对$i$$i$的影响是$\frac{1}{k}$$\frac{1}{k}$。

把$\overrightarrow{s}$$\vec s$（被认同者的观点值）与$A^{\ast }$$A^*$里的第$i$$i$行（被认同者对节点$i$$i$的影响分量）做点乘，就可以得到节点$i$$i$的新观点值。具体操作矩阵向量乘法时，我们只需转置$\overrightarrow{s}$$\vec s$：

迭代进行以上两个矩阵向量乘法，直到稳定。

9.2.2 编程实现与要点说明

首先仍然是读取有向图文件，存储在矩阵A里，读取初始观点向量，存储在向量S里。具体代码省略，参见1.2.1.2。我使用的数据文件如下：

xxxxxxxxxx
24
1
>>> 请输入有向图邻接矩阵文件名称（e.g. net1.dat, net2.dat）：net2.dat
2
>>> 有向图：
3
>>> [[0 1 0 1 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0]
4
>>>  [0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0]
5
>>>  [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0]
6
>>>  [1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0]
7
>>>  [0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0]
8
>>>  [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0]
9
>>>  [0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
10
>>>  [1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0]
11
>>>  [0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1]
12
>>>  [1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0]
13
>>>  [0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 0 1 0 0]
14
>>>  [1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0]
15
>>>  [0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0]
16
>>>  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0]
17
>>>  [0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0]
18
>>>  [0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0]
19
>>>  [0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 1]
20
>>>  [0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
21
>>>  [0 1 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 0]
22
>>>  [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]]
23
>>> 请输入认识初值向量文件名称（e.g. s1.dat, s2.dat）：s2.dat
24
>>> 初始观点向量：[ 5 32  2  4  5 10 21  3  2  6  8  3  1  9 23 45  2  3  9 11]

接着，我们来标准化矩阵，存储为A_sd。

xxxxxxxxxx
5
1
A_sd = np.zeros((ny,nx))
2
for i in range(ny):
3
    row = A[i]
4
    recognition_sum = np.sum(row)
5
    A_sd[i] = row / recognition_sum

迭代计算DeGroot共识。如前所述，我们应该转置S，再把A_sd和它做点乘。但是，为了书写的简便（主要是便于后面计算PageRank时书写方便），我没有转置S，而是转置了A_sd、得到A_trans，并且把向量S放在了左边、矩阵A_trans放在了右边。这样计算得到的结果是一样的。不过，严格按照数学中矩阵向量乘法的规定，还是应该如上操作。

xxxxxxxxxx
2
1
A_trans = np.transpose(A_sd)
2
S_initial = np.copy(S)

在每一轮，我们点乘S_original和A_trans，得到新的观点结果S。

xxxxxxxxxx
5
1
cnt = 0
2
while True:
3
    cnt += 1
4
    S_original = np.copy(S)
5
    S = np.dot(S, A_trans)

比较更新前后的观点向量，如果每一维度的值前三位小数不发生变化，我们就认为观点的迭代更新达成了稳定。

xxxxxxxxxx
11
1
    flag = True
2
    for i in range(n):
3
        s_original = '%.3f' % S_original[i]
4
        s = '%.3f' % S[i]
5
        if s_original != s:
6
            flag = False
7
    if flag == True:
8
        break
9
S_output = ['%.3f' % s for s in S]
10
print('*** DeGroot 共识结果：')
11
print(np.array(S_output))

xxxxxxxxxx
2
1
>>> *** DeGroot 共识结果：
2
>>> ['11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858' '11.858']

迭代计算PageRank。如前所述，我们应该转置A_sd和V，再把二者做点乘。但是，为了书写的简便，我没有做转置，而是把向量V放在了左边、矩阵A_sd放在了右边做点乘。

xxxxxxxxxx
6
1
V = np.array([1/n for i in range(n)])
2
cnt = 0
3
while True:
4
    cnt += 1
5
    V_original = np.copy(V)
6
    V = np.dot(V, A_sd)

比较更新前后的价值向量，如果每一维度的值前五位小数不发生变化，我们就认为价值的迭代更新达成了稳定。之所以两次判定稳定所取的小数位数不同，是因为，小数位数相同时，价值向量的有效位数比观点向量更少。

xxxxxxxxxx
11
1
    flag = True
2
    for i in range(n):
3
        v_original = '%.5f' % V_original[i]
4
        v = '%.5f' % V[i]
5
        if v_original != v:
6
            flag = False
7
    if flag == True:
8
        break
9
print('*** PageRank: ')
10
V_output = ['%.3f' % v for v in V]
11
print(np.array(V_output))

xxxxxxxxxx
2
1
>>> *** PageRank: 
2
>>> ['0.032' '0.038' '0.051' '0.038' '0.061' '0.062' '0.053' '0.004' '0.174' '0.056' '0.012' '0.030' '0.021' '0.043' '0.013' '0.123' '0.078' '0.036' '0.017' '0.059']

最后，我们使用PageRank对初始观点加权求和np.dot(V,S_initial)：

xxxxxxxxxx
2
1
consensus = np.dot(V,S_initial)
2
print('*** PageRank 加权初值求和结果：%.3f' % consensus)

xxxxxxxxxx
1
1
>>> *** PageRank 加权初值求和结果：11.858

基于PageRank算法得到的社会共识与DeGroot共识一致，本作业的理论假设得到了检验。

<< 返回本书主页
<< Back to the afterword page