<< 返回本书主页
<< Back to the afterword page

7 网络中的级联行为

吕汶桧 Wenhui Lyu

Jan. 2022

codes

7.1 背景问题

网络级联（network cascades）是传播学的重要理论。每个人是否接受一个新事物，受到周围人的极大影响，这进而影响了新事物在社会中的扩散。

如果我周围有更多人使用新产品$A$$A$，我也更倾向于放弃原来使用的产品$B$$B$，转而使用$A$$A$。这可能是因为

• 别人选择$A$$A$，我才有场合接触到和$A$$A$有关的信息，也更容易对$A$$A$产生信心。
• 和朋友们使用同样的产品更方便分享和协作（协调博弈，见下）。

周围人的影响可以用两种模型在社会网络中进行模拟：两个模型都假设一开始有几个初用节点率先使用了$A$$A$（他们大多是一些狂热分子），

• 随机模型：已激活节点以一定概率成功激活其邻居；
• 门槛模型：未激活节点的已激活邻居达到一定数目，该节点就被激活。

在门槛模型中，门槛值可以用协调博弈理论计算。我们考虑正在使用产品$B$$B$的节点$v$$v$，ta在社会网络中有$d$$d$个邻居。考虑邻居$w$$w$，节点$v$$v$和邻居$w$$w$之间存在协调博弈，其收益矩阵为

		节点w
		产品A	产品B
节点v	产品A	a, a	0, 0
	产品B	0, 0	b, b

节点$v$$v$的总回报等于她与所有邻居在此意义下博弈的综合结果。设ta的邻居使用$A$$A$的占比为$p$$p$。当选用$A$$A$的收益$\ge$$\geq$选用$B$$B$的收益时，亦即，当

时，节点$v$$v$会选用$A$$A$，否则会选用$B$$B$。也就是说，节点$v$$v$选用$A$$A$的门槛值$q={\displaystyle \frac{b}{a+b}}$$q=\dfrac{b}{a+b}$。

考虑产品$A$$A$在社会网络中扩散达成稳定的情况，此时所有节点与周围节点的协调博弈达成均衡。什么条件下，网络中节点将会全部放弃B，逐步转而选择A，实现采用A的完全级联？什么情况下，A在网络中停止了扩散，仅仅达成不完全级联？根据前文的分析，直接的回答是：剩下的每个采用$B$$B$节点的$A$$A$邻居数占比都不够大，小于门槛 $q={\displaystyle \frac{b}{a+b}}$$q = \dfrac{b}{a+b}$。

下图是一个形象的示意，采用$B$$B$的节点集合“抱团很紧”（其中的节点都没有足够的已激活邻居），$A$$A$攻不进去。除去初用节点，某种“密度”足够大的相关节点集合或“聚簇”，是级联进行不下去的关键。

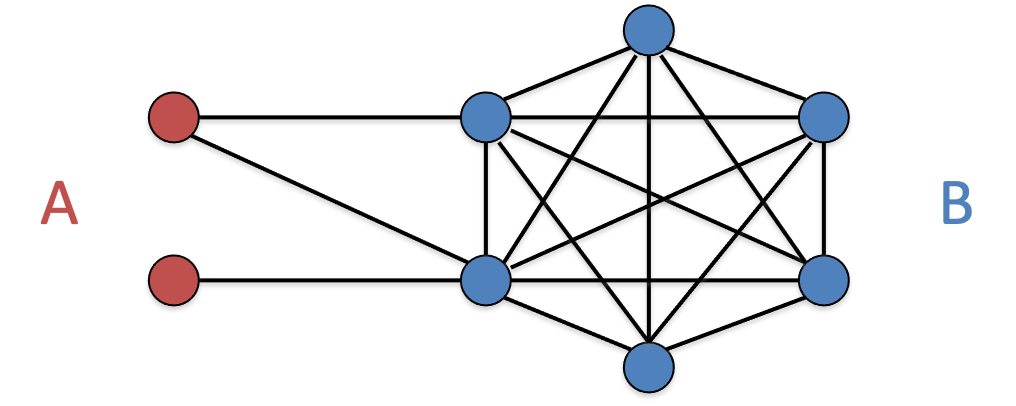
我们定义密度为$r$$r$的聚簇：一个节点集合，其中每个节点至少有占比$r$$r$的邻居节点也在这集合中。

设网络中一个初用节点集$S$$S$采用$A$$A$，删去$S$$S$后的剩余网络的其他节点采用$B$$B$，且它们改用$A$$A$的门槛值为$q$$q$。基于$S$$S$能够实现一个完全级联，当且仅当剩余网络中不存在密度大于$1-q$$1-q$的聚簇。

网络级联理论对于理解新产品推广很有帮助。课上，我们做了一个小练习：给定一个社会网络，选取哪些节点入手来推广新产品，会有最好的效果。

此外还有一个问题是，网络级联是否一定会终止？级联过程会不会震荡（改用$A$$A$的人后来又回到$B$$B$）？答案是，假设初用节点永不变色，后来每一时刻，每个节点的邻居中使用$A$$A$的人不会变少，级联过程就不会发生震荡，级联一定会终止。

除了新产品的推广以外，网络级联理论还能用来解释行为的扩散。当周围有足够多的人采取一项行动的时候（尤其是比较冒险的行动），一个人才有足够的意愿或勇气这样做。这样，周围的人的行为就扩散到了ta身上。这个人采取行动后，它又会进一步在ta的邻居中间扩散。 这件事的反面是“沉默的螺旋”：由于每个人都不敢率先采取行动或公开意见，尽管很多人都或多或少希望一件事发生，但都保持了沉默。

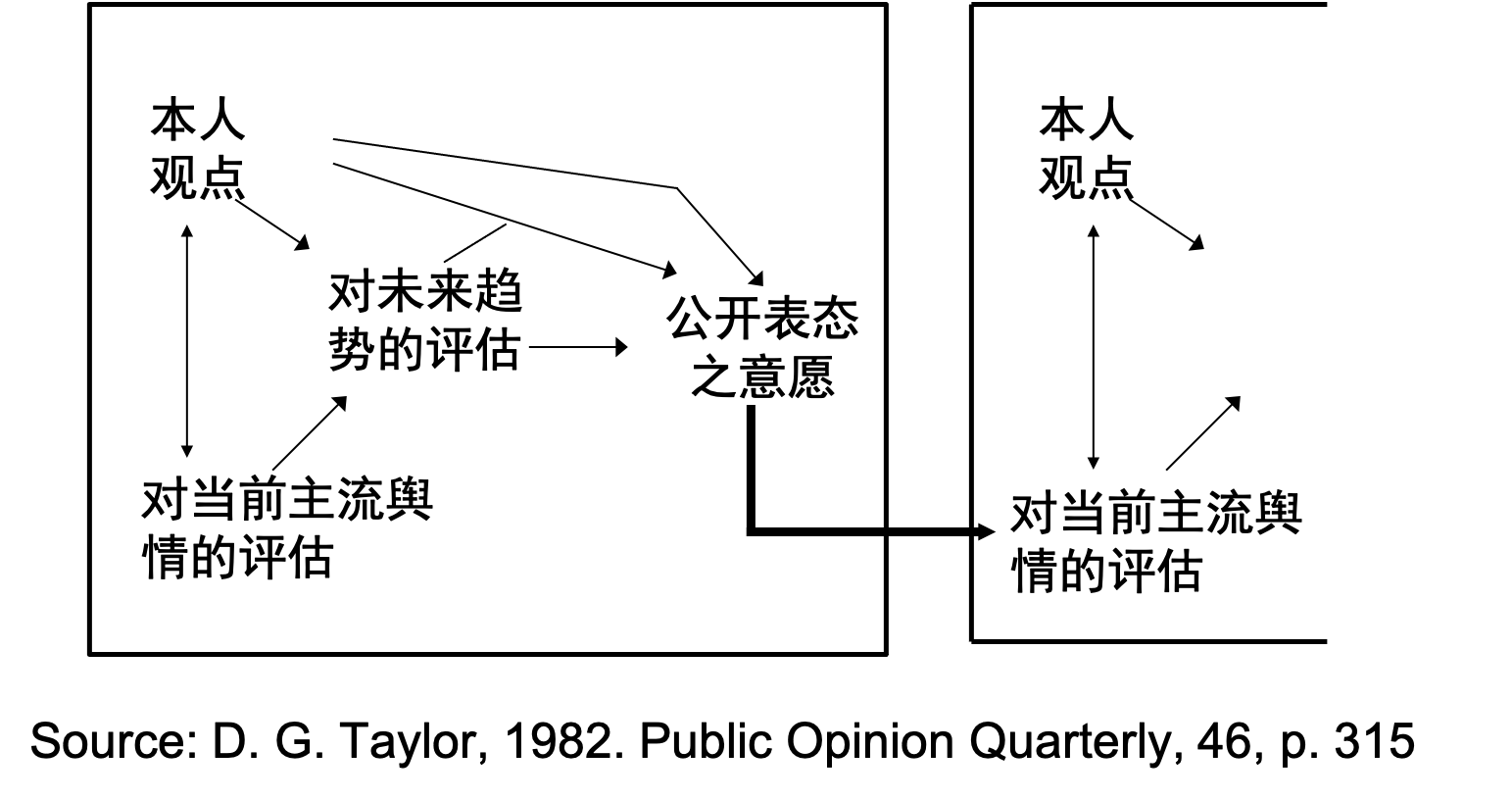
在不同类型的网络级联中，弱关系和强关系发挥了不同的作用：

• 弱关系对于信息传播有很重要的作用，如工作机会、在线视频、各种开放信息；
• 但对于一个行为的传播，特别是潜在成本较高的行为（例如请总裁辞职等有风险的活动），弱关系作用较小（弱关系往往是“捷径”（local bridge）（见2.1 背景问题），容易遇到聚簇的阻碍）。

7.2 计算实践：网络级联过程的仿真

codes

7.2.1 作业描述与算法思路

给定一个图的邻接矩阵$A$$A$、初用节点集$S$$S$、门槛值$q$$q$，模拟网络级联过程，输出从$S$$S$开始每一步级联得到的新节点，直到停止。

我们的模拟采用门槛模型。在每一步级联中，我们只需要关心：尚未激活的节点的邻居是什么情况，ta的邻居有多少人已被激活，这是否足以激活ta？

7.2.2 编程实现与要点说明

首先，读取文件，将邻接矩阵存储在numpy 2d-array A中，并要求用户输入门槛值q。代码略，与1.2.1.2类似。此外，我们还需要让用户输入初用节点集合，存储在列表变量users里：

xxxxxxxxxx
16
1
while True:
2
    S_input = input('请输入初用集（0–%i之间的自然数，用半角逗号分开）：' % (n-1))
3
    try:
4
        S_input = S_input.strip()
5
        S_list_str = S_input.split(',')
6
        S_list = []
7
        for S in S_list_str:
8
            S = S.strip()
9
            S = int(S)
10
            S_list.append(S)
11
    except:
12
        print('输入格式不正确。', end = '')
13
        continue
14
    break
15

16
users = S_list

初始值的一个例子如下：

xxxxxxxxxx
3
1
>>> 请输入矩阵名称（net1.dat / net2.dat / net3/dat）：net2.dat
2
>>> 请输入初用集（0–16之间的自然数，用半角逗号分开）：7,10,12
3
>>> 请输入门槛值（0–1之间的小数）：0.3

分析邻接矩阵，把每个节点的朋友有哪些存储在字典变量friends_all里，这方便我们逐节点分析邻居的激活情况。

xxxxxxxxxx
8
1
friends_all = {}
2
for i in range(n):
3
    friends_ind = []
4
    for j in range(n):
5
        edge = A[i][j]
6
        if edge == 1:
7
            friends_ind.append(j)
8
    friends_all[i] = friends_ind

级联开始。每一步级联中，我们跳过已经在使用新产品的人，逐节点分析剩下的人的邻居。

xxxxxxxxxx
9
1
rnd = 0
2
print('一开始的新用户：', end = '')
3
print(users)
4
while True:
5
    rnd += 1
6
    new_users = []
7
    for i in range(n):
8
        if i in users:
9
            continue

当节点i的邻居中，使用新产品的占比大于门槛值时，亦即len(friends_users) / len(friends_ind) >= q时，ta就会转而使用新产品。

xxxxxxxxxx
6
1
        friends_ind = friends_all[i] # all friends
2
        friends_users = [j for j in friends_ind if j in users] # friends who are using the new app
3
        influence = len(friends_users) / len(friends_ind) # the portion of friends who are using the new app
4
        if influence >= q: # willing to switch
5
            new_users.append(i)
6
    users += new_users

当已激活节点无法再激活新的节点new_users == []，级联结束，网络达成稳定。

xxxxxxxxxx
5
1
    if new_users == []:
2
        print('级联结束。')
3
        break
4
    print('第%i轮的新用户：' % rnd, end = '')
5
    print(new_users)

在上述初始值的例子里，级联过程输出如下

xxxxxxxxxx
7
1
>>> 一开始的新用户：[7, 10, 12]
2
>>> 第1轮的新用户：[4, 11, 13, 14, 16]
3
>>> 第2轮的新用户：[3, 6, 9, 15]
4
>>> 第3轮的新用户：[5, 8]
5
>>> 第4轮的新用户：[1]
6
>>> 第5轮的新用户：[0, 2]
7
>>> 级联结束。

<< 返回本书主页
<< Back to the afterword page