<< 返回本书主页
<< Back to the afterword page

5 匹配市场

吕汶桧 Wenhui Lyu

Jan. 2022

codes

5.1 背景问题

偏好卖家图

亚当斯密提出，市场经济就像有一个“无形之手”，把各方都安排妥当。本节课我们的任务就是把这一理论模型化。

考虑如下一个情境：要把一堆物品分配给一群人，不同人的偏好可能发生冲突，如何分配是最优的？为了简化问题，我们考虑一个更具体的情境：把$n$$n$件物品一一分配给$n$$n$个人。

我们把每个人对每个物品的偏好，抽象为一个出价（估值）矩阵，买家$i$$i$对物品$j$$j$的出价$v_{ij}$$v_{ij}$越高，意味着买家$i$$i$越想要物品$j$$j$。此外，每种物品的价格也各不相同，这构成了一个价格矩阵，物品$j$$j$的价格用$p_j$$p_j$表示。对于每一买家$i$$i$，我们可以找出他最想要的物品$j$$j$。具体地，我们要找出$v_{ij}-p_j$$v_{ij}-p_j$的最大值，因为这个差价定义了买家$i$$i$能从物品$j$$j$上获得的效用。

为了更形象地表示这一市场里每个人的的偏好情况，我们用一个二部图表示买家和物品，下图中左侧节点为物品（或“卖家”），右侧节点为买家。对于每一买家$i$$i$，在ta与ta最想要的物品$j$$j$之间做边（对应最大差价）。这样做出的图，就定义了体现买方喜好的一种二部图，称为“偏好卖家图”。

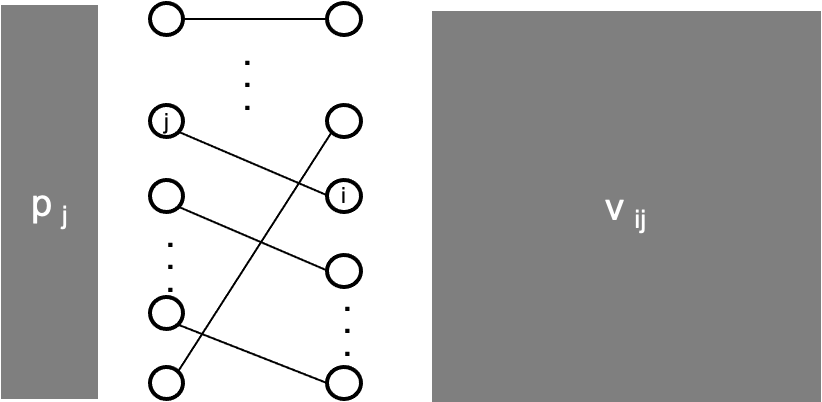
如果这一二部图里，每个买家的偏好恰好互不冲突，这一市场就存在“合理分配”。

以“物以稀为贵”促成“合理匹配”

对于一个特定的市场，亦即，对于特定的价格矩阵和特定的出价矩阵，不一定存在“合理分配”。为了解决这一问题，我们需要引入一个新的理论假设，“物以稀为贵”：如果买家的一个子集S所表达的偏好物品子集N(S)比S小，说明N(S)中的物品没法在S中无冲突地安排，意味着“稀有了”“紧俏了”，于是应该加价。这样的S称为“受限组”。

以“物以稀为贵”促成“合理匹配”的全过程就是，对全市场里所有紧俏的物品如此操作，不断迭代，直到这一市场存在“合理分配”。

我们设所有物品的初始价格为$0$$0$，实现合理分配时的最终价格，由偏好矩阵决定，越受欢迎的物品价格越高。

以下图为例，$a$$a$、$b$$b$、$c$$c$的初始价格都为$0$$0$。但此时，大家都想要物品$a$$a$。也就是说，存在买家受限组$S=\{x,y,z\}$$S=\{x,y,z\}$，此时的受限组邻居$N(S)=\{a\}$$N(S)=\{a\}$。

物品$a$$a$紧俏，我们就把$p_a$$p_a$从$0$$0$提高到$1$$1$。提价后，重新画偏好卖家图如下：

迭代操作，直到该市场存在合理分配，没有买家受限。

这一市场在价格向量为$(3,1,0)$$(3,1,0)$时出现合理分配，我们把$(3,1,0)$$(3,1,0)$称为清仓价格。

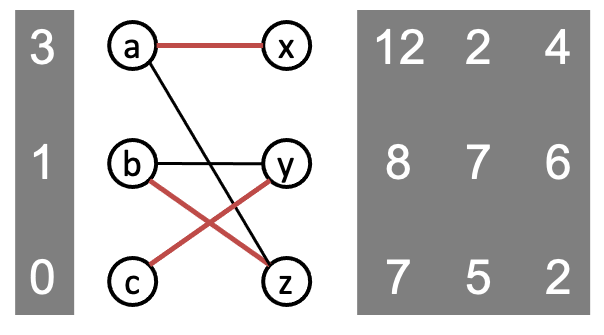
p.s. 当一个情境存在多个受限组时，选择哪一个受限组进行操作可能会影响最终的清仓价格，这意味着清仓价格不唯一。

对匹配算法的反思

我们可以证明，如此找出的合理分配，实现了社会福利的最大化。

给定清仓价格（$p$$p$）和估值矩阵（$V$$V$），每个买家从买到的物品身上获得的效用（估值与价格的差值）的总和$max(\sum \text{差}\text{价})$$max(\sum差价)$是最大的，这一总和可以如此表达：

对于任意一种分配方式，总有：

因此，

给定一组价格，匹配算法取到$max(\sum \text{差}\text{价})$$max(\sum差价)$时，也同时取到了$max(\sum \text{对}\text{应}\text{估}\text{值})$$max(\sum对应估值)$。

这个算法有更广泛的应用：

• 给定一个$n\times n$$n\times n$的整数矩阵，从中选择$n$$n$个不同行不同列元素，使得加和最大。
• 每个人给出自己的偏好序列，我们也可以依据这一偏好人为地赋值，从而使用这一算法进行物品分配。

另一个问题是，为什么提价时我们以$1$$1$为单位呢？这是因为估值矩阵里的价差最小为$1$$1$。提价$+1$$+1$，才能把价差$1$$1$的偏好区别体现在市场分配上。如果提价时$+2$$+2$，可能导致一下子提价太多，大家都不想要这个商品了。

此外，匹配算法过程总能结束，我们可以给出一个数学证明。

定义一个势能函数：

在匹配算法运行过程中，$P$$P$逐渐减小：每一次进行操作时，$+1$$+1$一致地发生在买方受限组$S$$S$关注的所有卖方$N(S)$$N(S)$上；由于$S$$S$严格大于$N(S)$$N(S)$ ，$P$$P$每次增$|N(S)|$$|N(S)|$，至少减$|S|$$|S|$，即$P$$P$单调递减。

但$P$$P$又不能无限制地减下去，我们可以证明$P\ge 0$$P\geq0$恒成立：

$P$$P$的减小总有个头，所以匹配算法一定能结束。

总之，我们把经济学中的经典概念，例如理性人、价格、供需关系、物以稀为贵、均衡、社会最优，做出了生动的表达，使用的是简单图论语言和计算过程描述，例如偏好卖家图、受限组、迭代调整价格、结束条件。

5.2 计算实践：实现匹配市场算法

codes

5.2.1 作业描述与算法思路

为了把这一模型放在一个更具体的场景中，李老师给全班的同学发放问卷，让班上的11个同学给出对11本书的出价，得到具体的出价矩阵如下：

序号	西方哲学史	中国历代政治得失	尤利西斯	致命的自负	车浩的刑法题	深度学习	时间序列分析	期权、期货及其他衍生产品	红书	历史的逻辑	海德格尔哲学概论
1	0	0	10	5	0	25	20	10	0	0	0
2	5	10	1	1	0	40	4	0	55	10	30
3	0	0	0	10	0	0	0	5	0	5	0
4	20	0	60	20	0	60	0	0	0	30	10
5	40	10	30	20	5	25	40	0	35	30	13
6	10	10	0	10	20	0	20	0	0	20	10
7	55	30	50	10	0	50	50	0	80	20	30
8	0	0	0	0	0	30	30	70	0	0	0
9	0	20	10	15	30	15	0	0	5	5	0
10	10	0	0	35	0	10	55	45	0	0	0
11	20	10	20	0	0	10	0	0	0	10	20

本次作业就是找出以上市场的最优匹配。我们输入以上估值矩阵，输出一组清仓价格、对应的偏好卖家图（二部图）上的一个完整匹配、对应的社会最优（值）。

根据前文，先设所有书的初始价格为零，根据估值矩阵和价格矩阵确定偏好卖家图，判断合理匹配是否存在，如果存在就输出合理匹配，不存在就找出受限组邻居（大家都想要的物品），对受限者邻居提高一个单位的价格。迭代运行以上算法，直到实现完整匹配。

编程中存在几个难点：

• 如何判断当前市场中是否存在完整匹配？如果不存在，如何返回一个受限组和其对应的受限组邻居？这一部分不在我们的作业要求中，李老师给了我们一个函数perfect_match供调用。
• 如何根据估值矩阵或价格矩阵生成偏好卖家图？首先要找出买家$i$$i$最想要哪个物品。我们遍历所有物品，计算买家$i$$i$的估值和价格之差，找出差价最大者$j$$j$即可。而至于二部图的数学表示，以如下的矩阵（记为$A$$A$）为例：

$i_1$$i_1$想要$j_1$$j_1$（$A[i_1][j_1]=1,A[j_1][i_1]=1$$A[i_1][j_1]=1,A[j_1][i_1]=1$），$i_2$$i_2$想要$j_2$$j_2$，$i_3$$i_3$想要$j_3$$j_3$。二部图矩阵的左上和右下总为0，因为一部内部没有边；而左下和右上表示不同部的两个元素之间的关系，可以是0，也可以是1。因此，二部图矩阵可以表示为以下一般形式：

5.2.2 编程实现与要点说明

李老师提供了perfect_match函数：输入表示偏好卖家图的二部图，如果存在完整匹配，返回True和完整匹配边集{ (i,matched[i]) for i in range(n) }；如果不存在，返回False和一个受限组邻居{matched[n] for n in bfs_queue if n != i}。

xxxxxxxxxx
51
1
"""
2
程序提供perfect_match函数，该函数接收一个2n个节点二部图的邻接矩阵，前n个节点可认为二部图左部，后n个节点为右部。
3
若存在完美匹配，函数返回真及一个完美匹配的边集合，否则返回假并给出右部节点的一个受限集关联的左部邻居节点集合。
4
基本思路为对左部未匹配节点作交替BFS，找增广路径，详见教材10.6或"匈牙利算法"。
5
"""
6
def perfect_match(matrix):
7
    node_num = len(matrix)
8
    node_left = node_num >> 1
9
    # 邻接矩阵转化为邻接表，对稀疏图可提高下面循环的效率
10
    graph = [{i for i in range(node_num) if matrix[j][i] == 1} for j in range(node_num)]
11
    checked = [-1] * node_num  # 记录某节点i是否已在checked[i]节点为根的先宽搜索树中
12
    prev = [-1] * node_num     # 记录交替路径中某右部节点的上一个右部节点，左部节点已被matched记录
13
    matched = [-1] * node_num  # 记录某节点匹配的节点
14
    for i in range(node_left, node_num):
15
        if matched[i] != -1:   # i应是某尚未匹配的右部节点
16
            continue
17
        # 先宽搜索队列只记录右部节点，这些节点是左部节点通过已有匹配边一一对应来的
18
        bfs_queue = [i]
19
        pos = 0                # 记录遍历队列的当前位置
20
        flag = False           # 一次搜索找到一条增广路径即完成
21
        prev[i] = -1           # i记录为路径起点
22
        while pos < len(bfs_queue) and not flag:
23
            node = bfs_queue[pos]
24
            # node是右部节点，j是与之相邻的左部节点
25
            for j in graph[node]:
26
                if checked[j] == i:
27
                    continue
28
                checked[j] = i
29
                # 将j匹配的右部节点加入队列继续搜索
30
                if matched[j] > -1:
31
                    bfs_queue.append(matched[j])
32
                    prev[matched[j]] = node
33
                # j没有匹配的右部节点说明找到增广路径
34
                else:
35
                    flag = True
36
                    t1, t2 = node, j
37
                    while t1 != -1:
38
                        t3 = matched[t1]
39
                        matched[t1] = t2
40
                        matched[t2] = t1
41
                        t1 = prev[t1]
42
                        t2 = t3
43
                if flag:
44
                    break
45
            pos += 1
46
        # 该右部节点无法匹配说明不存在完美匹配，此时搜索队列即组成一个受限组。
47
        # 因为i未能匹配说明前面没有从i出发找到增广路径，即i的搜索树中左部节点总是通过已有匹配一一对应到其他右部节点，
48
        # 因此这些右部节点和i恰比它们的邻居左部节点多1
49
        if matched[i] == -1:
50
            return False, {matched[n] for n in bfs_queue if n != i}
51
    return True, {(i, matched[i]) for i in range(node_left)}

我们的任务，就是要根据出价矩阵和价格矩阵生成偏好卖家图，调用perfect_match函数，对受限组邻居进行加价；迭代这一过程，直到出现完整匹配。

第一步仍然是读取文件中的出价矩阵，存储在numpy 2d-arraybids里，具体代码类似1.2.1.2，数据见5.2.1。初始价格为[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]。

根据出价矩阵和价格矩阵，我先生成一个表示偏好卖家图的二部图。

xxxxxxxxxx
5
1
round = 0
2
while True:
3
    round += 1
4
    print('- - - - - - - - - - - - - - - - - - round %i - - - - - - - - - - - - - - - - - -' % round)
5
    market = np.zeros((items + buyers,items + buyers))

具体地，对于买家$i$$i$，我找出差价最大的物品，存储在bid_item这一列表里（可能有多个）。

xxxxxxxxxx
13
1
    for i in range(buyers):
2
        diff_max = bids[i][0] - prices[0]
3
        bid_item = [0]
4
        for j in range(1, items):
5
            # the starting-point of comparison: the first item
6
            bid = bids[i][j]
7
            diff = bid - prices[j]
8
            # compare to get the most wanted item
9
            if diff > diff_max:
10
                diff_max = diff
11
                bid_item = [j]
12
            elif diff == diff_max:
13
                bid_item.append(j)

market二部图里，前items个编码表示物品，剩下的编码表示买家。买家$i$$i$想要物品$k$$k$在market二部图里就表示为

xxxxxxxxxx
3
1
        for k in bid_item:
2
            market[items + i][k] = 1
3
            market[k][items + i] = 1

生成二部图market后，我就可以调用perfect_match函数。当市场不存在完整匹配时，我就对perfect_match返回的受限组邻居nb_set进行提价。

xxxxxxxxxx
8
1
    if perfect_match(market)[0]:
2
        ...
3
        break
4
    print('未能清仓。Prices for the next round:', end = ' ')
5
    nb_set = perfect_match(market)[1]
6
    for i in nb_set:
7
        prices[i] += 1 
8
    print(prices)

第一轮的运行结果如下：

xxxxxxxxxx
2
1
>>> - - - - - - - - - - - - - - - - - - round 1 - - - - - - - - - - - - - - - - - -
2
>>> 未能清仓。Prices for the next round: [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]

迭代运行多轮，直到perfect_match(market)[0] = True，实现清仓。输出清仓价格：

xxxxxxxxxx
3
1
    if perfect_match(market)[0]: # succeed clearing
2
        print('清仓价格：', end = '')
3
        print(prices)

xxxxxxxxxx
1
1
>>> 清仓价格：[10.  0. 10.  0.  0. 20. 15.  5. 35.  0. 10.]

接着就是输出匹配结果、计算社会福利。计算社会福利时，我需要把每个人为ta买到的商品的估值final_price加总。

xxxxxxxxxx
14
1
        wellBeing = 0
2
        bought_dict = {}
3
        for item in perfect_match(market)[1]:
4
            bought = item[0]
5
            buyer = item[1] - buyers
6
            final_bid = bids[buyer][bought]
7
            final_price = prices[bought]
8
            final_diff = final_bid - final_price
9
            bought_dict[buyer] = [bought, final_price, final_diff]
10
            wellBeing += final_bid
11
            print('右边买家%i与左边卖家%i匹配，他该支付%i，得最大差价%i。' \
12
                % (buyer, bought, final_price, final_diff))
13
        print('优化的社会福利为：', end = '')
14
        print(wellBeing)

具体结果如下：

xxxxxxxxxx
12
1
>>> 右边买家10与左边卖家1匹配，他该支付0，得最大差价10。
2
>>> 右边买家8与左边卖家4匹配，他该支付0，得最大差价30。
3
>>> 右边买家4与左边卖家0匹配，他该支付10，得最大差价30。
4
>>> 右边买家2与左边卖家3匹配，他该支付0，得最大差价10。
5
>>> 右边买家0与左边卖家5匹配，他该支付20，得最大差价5。
6
>>> 右边买家1与左边卖家10匹配，他该支付10，得最大差价20。
7
>>> 右边买家7与左边卖家7匹配，他该支付5，得最大差价65。
8
>>> 右边买家9与左边卖家6匹配，他该支付15，得最大差价40。
9
>>> 右边买家5与左边卖家9匹配，他该支付0，得最大差价20。
10
>>> 右边买家6与左边卖家8匹配，他该支付35，得最大差价45。
11
>>> 右边买家3与左边卖家2匹配，他该支付10，得最大差价50。
12
>>> 优化的社会福利为：430

另外，我还提供了查询每个人应该买什么书的代码：

xxxxxxxxxx
12
1
        if fname.endswith('.csv'): # This part is needed only when the data file is a csv file (which has recorded students' preferences for books)
2
            while True:
3
                me = input('Which one is you? (input integers from 0 to 10)\nTo know which one Wenhui needs to buy, input 10.\ninput here: ')
4
                try:
5
                    me = int(me)
6
                    if me in range(11):
7
                        break
8
                except:
9
                    pass
10
                print('Wrong input.', end = ' ')
11
            bookBought = book_list[bought_dict[me][0]]
12
            print('I need to buy %s at the cost of %i, getting the largest difference of %i.' % (bookBought, bought_dict[me][1], bought_dict[me][2]))

输入我对应的编码，可以得到我应该买《中国历代政治得失》：

xxxxxxxxxx
4
1
>>> Which one is you? (input integers from 0 to 10)
2
>>> To know which one Wenhui needs to buy, input 10.
3
>>> input here: 10
4
>>> I need to buy 《中国历代政治得失》钱穆，三联书店 at the cost of 0, getting the largest difference of 10.

<< 返回本书主页
<< Back to the afterword page