<< 返回本书主页
<< Back to the afterword page

3 极化关系下网络结构的稳定平衡性

吕汶桧 Wenhui Lyu

Jan. 2022

codes

3.1 背景问题

本讲的主题是，社会网络在什么情况下是平衡的，什么情况下不是？

在一个社会中，两个人的关系可能是友善的，也可能是互相抱有敌意的。为了模拟这种现象，我们可以把社会网络中某两个节点之间的边，标注为正关系（友）或负关系（敌）。对于网络中的一个三角结构，我们就可以讨论它是否平衡。

• 平衡结构有以下两种。这在直观上也很好理解，如果三个人互为好友（左图），或者两个关系很好的人同时看不上第三个人（右图），是没有旁的因素打破这种关系的，这就可以长时间维持。

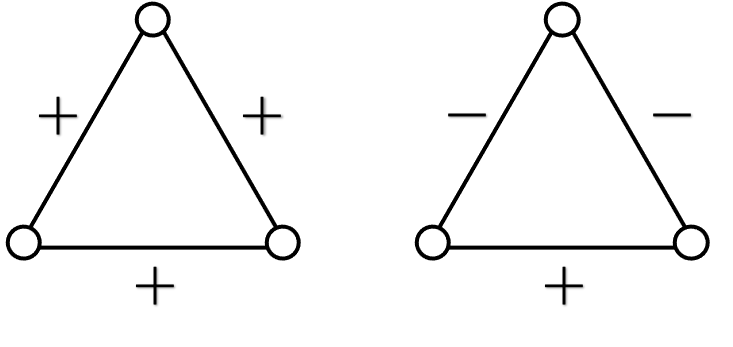
• 不平衡结构也是以下两种。如果两个人关系不好但有一个共同朋友（左图），这个共同朋友就很难做人，要么倒向其中一边，要么努力让他俩冰释前嫌。如果三个人互有敌意（右图），敌意稍轻的两个人就有动力联合起来，共同对付第三个人。

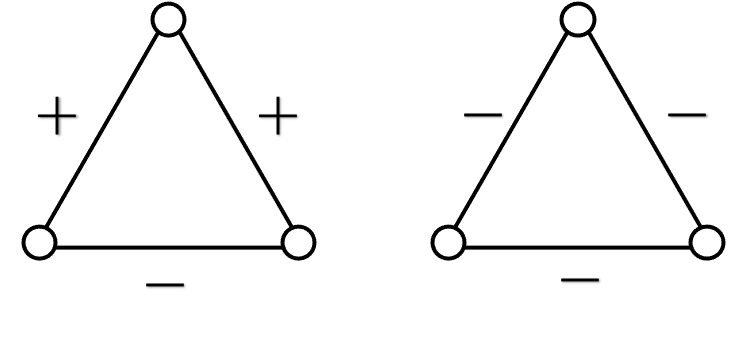
在一个社会网络中，如果所有三角关系都是平衡的，那么这个网络就是平衡的；否则，总有力量改变其中的某个三角关系，从而影响网络结构的平衡性。这个定义可以进一步操作化——结构平衡定理：

一个边标注完全图是平衡的，当且仅当它的所有边都是“＋”边或节点集能划分为两个子集，子集内部都是“＋”边，子集之间都是“－”边。

也就是说，这一网络要么全部是正关系，要么可以表示为如下的结构：

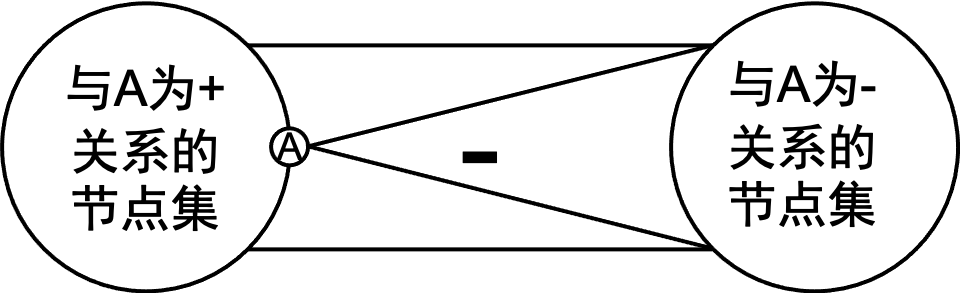
简单的归谬法就可以证明这一定理。如果左边的关系中存在负关系，设节点$B$$B$和节点$C$$C$之间为“－”边，那么$ABC$$ABC$就是“＋＋－”的不稳定关系。如果右边的关系中存在正关系，设节点$B$$B$和节点$C$$C$之间为“＋”边，那么$ABC$$ABC$就是“＋＋－”的不稳定关系。

可是，社会网络中并非所有节点之间都有边，不是所有边都身处一个或多个三角关系中，逐个考察三角关系的方法不再适用。对于不完全网络图，我们如此理解它的平衡状态：不会因为增加一条标注边，出现不可避免的不平衡三角子图。例如下图，当两个本无关系的人$B$$B$和$D$$D$，处在两个潜在的三角关系$ABD$$ABD$和$BCD$$BCD$中，$ABD$$ABD$要求$BD$$BD$为“＋”关系，$BCD$$BCD$要求$BD$$BD$为“－”关系。不管加上的$BD$$BD$边是什么，这幅图都会出现不平衡三角子图。

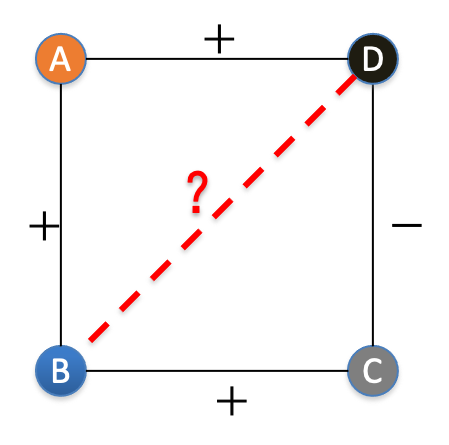
也就是说，一个平衡的不完全网络图，可以通过补充缺失的边（带极性），成为一个平衡的完全网络。根据结构平衡定理，平衡的不完全网络图的定义也可以进一步操作化：

若已有边不全是“＋”，则节点可以分成两组，组内边均为“＋”，跨组边均为“－”。

3.2 计算实践：网络结构平衡性的判断

codes

3.2.1 作业描述与算法思路

接续上文，要判断不完全网络图是否平衡，我们已经有了一个操作化定理：

若已有边不全是“＋”，则节点可以分成两组，组内边均为“＋”，跨组边均为“－”。

但这距离算法化还有一定距离。为了算法化，我们还要进一步用到图论的知识：一个含有奇数个“－”的圈的节点不能被分成这样两组：每一组内部的关系都为“＋”，跨组的边均为“－”。

也就是说，如果图中存在一个含有奇数个“－”的圈，就没有可能将其节点安排到两个对立阵营中；反过来，若没有那样的圈，则总是可以将所有节点做两个阵营的划分。根据上述操作化定理，如果图中存在一个含有奇数个“－”的圈，该图就不平衡；反之就平衡。

为了更方便地判定网络中是否存在含有奇数个“－”的圈，我们可以整体考虑内部边均为“＋”的节点子集，因为它们并不会影响自己所在的圈有多少个“－”。把内部边均为“＋”的节点集合为一个“连通分量”，从而把网络简化为“简约图”。这样，简约图里所有的边都是“－”边。例如，下图左侧的不完全社会网络（红边为“＋”、黑边为“－”），就可以表示为右侧的简约图。

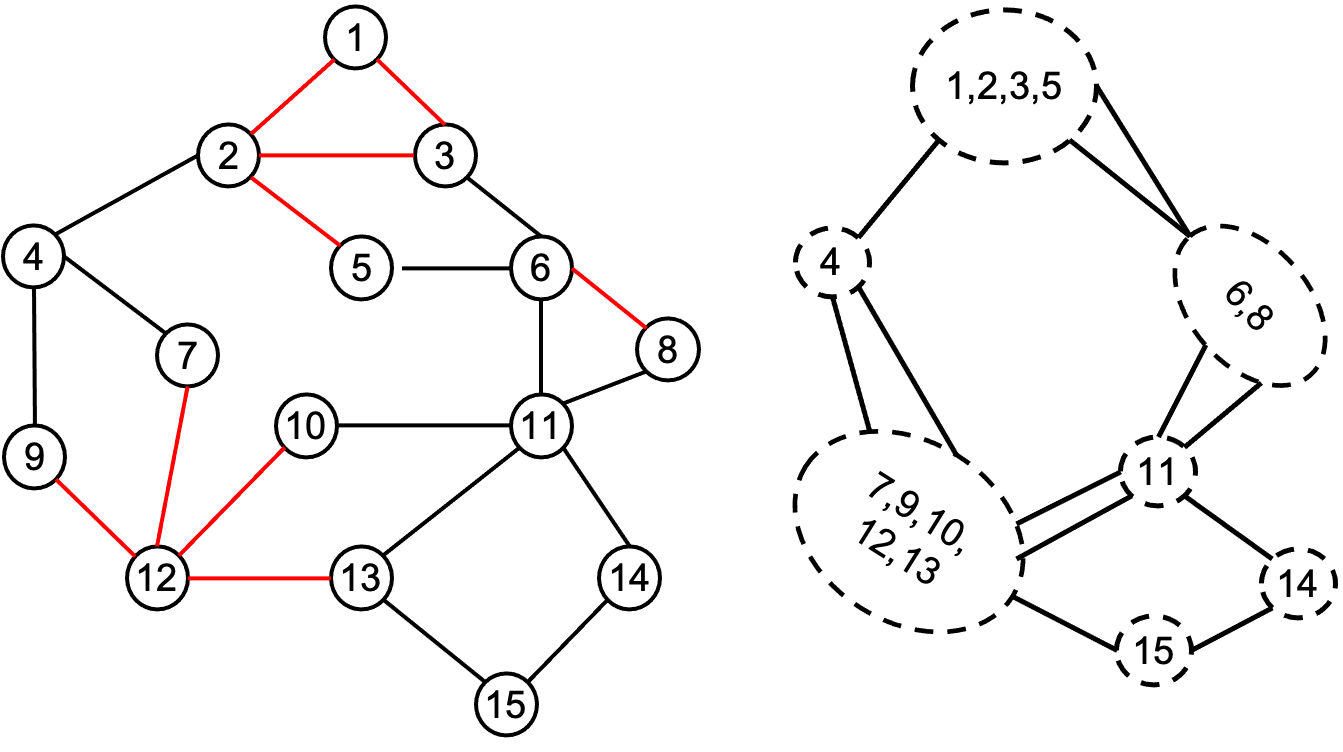
现在，我们只需要考虑简约图里有没有长度为奇数的圈。判定方式是“广度优先搜索”（Breadth First Search or BFS）。在下图的例子中，对左侧的图以节点$G$$G$为起点做广度优先搜索，所有节点被归入到1–3层里。

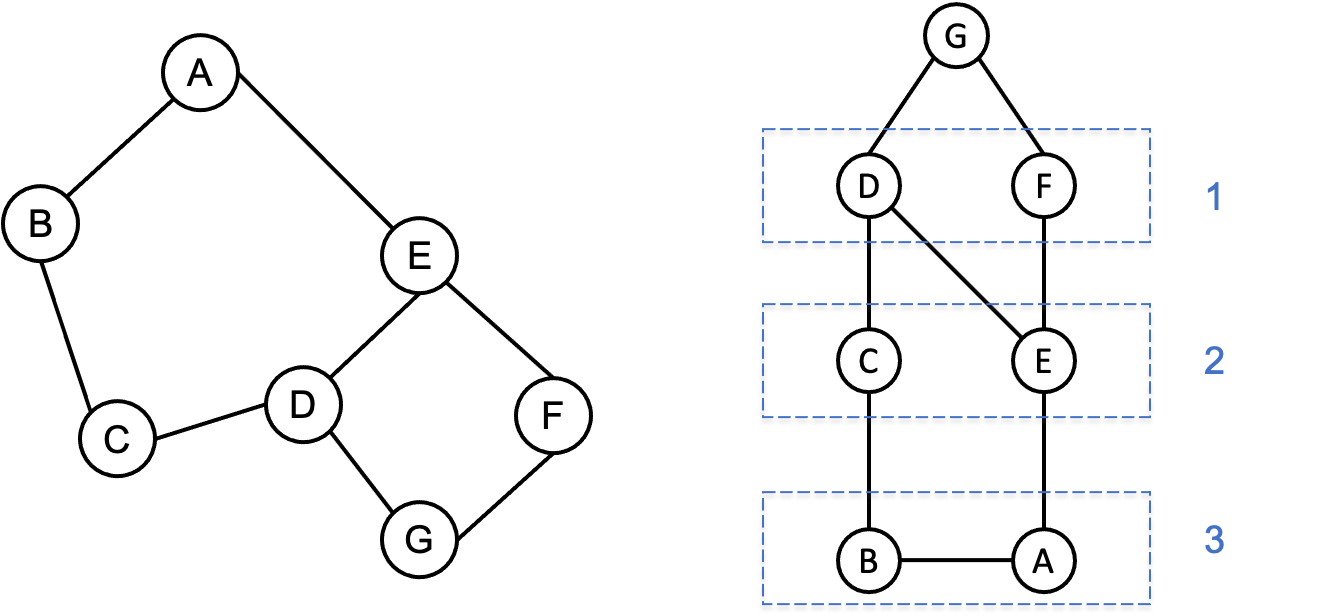
从广度优先搜索的结果可以看到，圈的形成有两种方式：

• 下位节点（层数更高的节点）与两个上位同层节点都有边（如$E$$E$与$D$$D$、$F$$F$都有边，形成圈$GFED$$GFED$）。这种方式方式形成的是偶数边的圈；因为，每个边都是跨层边，对于一组相邻层（如层$1$$1$和层$2$$2$），这个圈都会跨两次（如$DE$$DE$和$EF$$EF$就跨了层$1$$1$和层$2$$2$两次，形成圈$GFED$$GFED$）。
• 同层的两个节点之间有边（如$AB$$AB$，形成圈$DEABC$$DEABC$）。这种方式则会形成奇数边的圈，除了跨两次相邻层以外，这个圈还在层内有一条边（如$AB$$AB$，形成圈$DEABC$$DEABC$）。

这样，要判断不完全网络图是否平衡，我们只需要BFS结果中是否存在同层边。

3.2.2 编程实现与要点说明

首先，我们还是需要调用读取数据文件的函数，把邻接矩阵存储在一个numpy 2d-array array里。代码略，与1.2.1.2类似。一个数据文件的例子如下：

xxxxxxxxxx
16
1
输入矩阵文件名：./input/balance1.txt
2
[[ 0  1  1  0  0  0  0  0  0  0  0  0  0  0  0]
3
 [ 1  0  1 -1  1  0  0  0  0  0  0  0  0  0  0]
4
 [ 1  1  0  0  0 -1  0  0  0  0  0  0  0  0  0]
5
 [ 0 -1  0  0  0  0 -1  0 -1  0  0  0  0  0  0]
6
 [ 0  1  0  0  0 -1  0  0  0  0  0  0  0  0  0]
7
 [ 0  0 -1  0 -1  0  0  1  0  0 -1  0  0  0  0]
8
 [ 0  0  0 -1  0  0  0  0  0  0  0  1  0  0  0]
9
 [ 0  0  0  0  0  1  0  0  0  0 -1  0  0  0  0]
10
 [ 0  0  0 -1  0  0  0  0  0  0  0  1  0  0  0]
11
 [ 0  0  0  0  0  0  0  0  0  0 -1  1  0  0  0]
12
 [ 0  0  0  0  0 -1  0 -1  0 -1  0  0 -1 -1  0]
13
 [ 0  0  0  0  0  0  1  0  1  1  0  0  1  0  0]
14
 [ 0  0  0  0  0  0  0  0  0  0 -1  1  0  0 -1]
15
 [ 0  0  0  0  0  0  0  0  0  0 -1  0  0  0 -1]
16
 [ 0  0  0  0  0  0  0  0  0  0  0  0 -1 -1  0]]

第一步，我们先要把网络简化为简约图。先写一个函数cluster，找出节点$i$$i$所处的连通分量group，其中所有边都是“＋”边。这个函数用到了递归，我先以$i$$i$为起点，找到和它以“＋”边相连的节点$j$$j$，再以$j$$j$为起点做同样的操作（这其实也是“广度优先搜索”），直到找不到更多以“＋”边相连的节点。

xxxxxxxxxx
7
1
def cluster(array, i, group):
2
    group.append(i)
3
    for j in range(len(array[i])):
4
        if j not in group:
5
            if array[i][j] == 1:
6
                cluster(array, j, group)
7
    return group

循环调用cluster函数，每次的搜索起点是还未归入某一连通分量的节点，直到把网络中所有节点都归入某一连通分量。结果存储在groups中。

xxxxxxxxxx
15
1
groups = []
2
cnt = 0
3
start = 0
4
rest = [i for i in range(n)]
5
while True:
6
    groups.append([])
7
    groups[cnt] = cluster(array, start, groups[cnt])
8
    for j in groups[cnt]:
9
        rest.remove(j)
10
    if rest == []:
11
        break
12
    start = rest[0]
13
    cnt += 1
14
print('连通分量如下：')
15
print(groups)

以下是一个输出结果的例子：

xxxxxxxxxx
2
1
>>> 连通分量如下：
2
>>> [[0, 1, 2, 4], [3], [5, 7], [6, 11, 8, 9, 12], [10], [13], [14]]

寻找连通分量的过程，并未一一检查内部的所有边。以特定次序找“＋”得出的节点集合，在另一种找边的次序中可能存在“－”边。因此我们还需要重新检查一下连通分量内部是否有“－”边。如果有的话，我们可以直接确定这一网络不平衡，因为这一连通分量内部有“＋＋－”的不稳定关系。

xxxxxxxxxx
13
1
innerGroup = False
2
for group in groups:
3
    for a in range(len(group)):
4
        node1_1 = group[a]
5
        if innerGroup == False:
6
            for node1_2 in group[a+1:]:
7
                if array[node1_1][node1_2] == -1: 
8
                    innerGroup = True
9
                    break
10
if innerGroup == True:
11
    print('★★连通分量内部有负边，该网络不平衡。★★')
12
    print('★★★★该网络不是平衡网络。★★★★')
13
    sys.exit(0)

如果连通分量内部没有“－”边，我们就可以使用groups的信息生成简约图array2。我们检查连通分量之间是否有边（只可能是“－”边），从而确定表示简约图的矩阵在每一格应该填什么。有边就填1，无边就填0。

xxxxxxxxxx
17
1
array2 = np.zeros((cnt+1,cnt+1))
2
for i in range(len(groups)):
3
    group = groups[i]
4
    for j in range(i+1, len(groups)):        
5
        next = groups[j]
6
        edgeExist = False
7
        for node1 in group:
8
            if edgeExist == True:
9
                break     
10
            for node2 in next:
11
                if array[node1][node2] == -1: # 有边
12
                    array2[i][j] = 1 # 定义有边为1
13
                    array2[j][i] = 1
14
                    edgeExist = True
15
                    break
16
print('简约网络图如下：')
17
print(array2)

xxxxxxxxxx
8
1
>>> 简约网络图如下：
2
>>> [[0. 1. 1. 0. 0. 0. 0.]
3
>>>  [1. 0. 0. 1. 0. 0. 0.]
4
>>>  [1. 0. 0. 0. 1. 0. 0.]
5
>>>  [0. 1. 0. 0. 1. 0. 1.]
6
>>>  [0. 0. 1. 1. 0. 1. 0.]
7
>>>  [0. 0. 0. 0. 1. 0. 1.]
8
>>>  [0. 0. 0. 1. 0. 1. 0.]]

接着，我们对简约图做广度优先搜索：输入起点节点，输出搜索结果（每一层有哪些节点layers，节点之间的边有哪些layerCon）。这一过程依靠函数bfs完成。

xxxxxxxxxx
9
1
layers = []
2
layerCon = []
3
counted = [0] # 已经被搜索到的节点
4
def bfs(i_list, layerNum, array = array2):
5
    global layers
6
    global layerCon
7
    global counted
8
    layers.append([]) # 新建一层
9
    layerCon.append([])

搜索时，我用到了递归，搜索到下一层的节点j_list后，再以j_list里的节点为起点搜索再下一层，直到搜不到更多节点j_list == []。

​x
1
    j_list = [] # 下一层的节点
2
    for i in i_list:
3
        layers[layerNum].append(i)
4
        if len(counted) == len(array):
5
            break
6
        for j in range(len(array[i])):
7
            if j not in counted:
8
                if array[i][j] == 1:
9
                    layerCon[layerNum].append([i, j])
10
                    j_list.append(j)
11
    j_set = set(j_list)
12
    j_list = list(j_set) # 去除重复节点
13
    for j in j_list:
14
        counted.append(j)
15
    layerNum += 1
16
    if j_list != []:
17
        bfs(j_list, layerNum) # recursion, start from the next layer
18
    return layers, layerCon
19

20
layers, layerCon = bfs([0], 0)
21
print('layers:')
22
print(layers)
23
print('层间边：')
24
print(layerCon)

xxxxxxxxxx
4
1
>>> layers:
2
>>> [[0], [1, 2], [3, 4], [5]]
3
>>> 层间边：
4
>>> [[[0, 1], [0, 2]], [[1, 3], [2, 4]], [[3, 6], [4, 5]], []]

有了搜索结果，我们就可以两两检查每层内的节点，判断层间边是否存在。

xxxxxxxxxx
19
1
innerLayer = False
2

3
for layer in layers:
4
    layerI = layers.index(layer)
5
    for x in range(len(layer)):
6
        i = layer[x]
7
        for j in layer[x+1:]:
8
            if array2[i][j] == 1: # i与j之间有层间边
9
                innerLayer = True 
10

11
if innerLayer == True:
12
    print('★★层内有边，该网络不平衡。★★')
13
else:
14
    print('无层内边。')
15

16
if innerLayer == False:
17
    print('★★★★该网络为平衡网络。★★★★')
18
else:
19
    print('★★★★该网络不是平衡网络。★★★★')

存在层内边时，我们还可以用一个函数circleSpotter找出奇数圈：输入两个起点节点编码（初始为存在层内边的两个节点编码i和j）、它们在哪一层layerI、已经找到的奇数圈节点oddCir（初始为[i,j]）、广度优先搜索的结果layers和layerCon；返回所有奇数圈节点。

xxxxxxxxxx
1
1
def circleSpotter(i, j, layerI, oddCir, layerCon = layerCon, layers = layers):

定义一个局部函数nodeAdder，它的作用是，当我们找到起点节点所在的层内边edge后（如$i\to i2$$i\to i2$），我们把$i2$$i2$加入oddCir当中，并把$i2$$i2$确定为新的起点节点，以便进行下一轮搜索。

xxxxxxxxxx
6
1
    def nodeAdder(edge, x):
2
        for node in edge:
3
            if node != i and node in layers[layerI - 1]:
4
                oddCir.append(node)
5
                i2 = node
6
        return oddCir, i2

给定i和j，分别调用nodeAdder函数，沿着i和j所在的层间边，确定下一组起点节点（在更高层）i2和j2。

xxxxxxxxxx
13
1
    i_counted = False
2
    j_counted = False
3
    for edge in layerCon[layerI - 1]:
4
        if i in edge:
5
            if i_counted == True:
6
                continue
7
            oddCir, i2 = nodeAdder(edge, i)
8
            i_counted = True
9
        elif j in edge:
10
            if j_counted == True:
11
                continue
12
            oddCir, j2 = nodeAdder(edge, j)
13
            j_counted == True

以i2和j2为新的起点节点继续搜索（递归），直到两条搜索线路汇集于同一点i2 == j2。

xxxxxxxxxx
6
1
    layerI -= 1
2
    if i2 != j2:
3
        circleSpotter(i2, j2, layerI, oddCir) # recursion, start from upper layer
4
    oddCirSet = set(oddCir)
5
    oddCir = list(oddCirSet) # make sure there aren't duplicates
6
    return oddCir

对于每一条层间边，我们都可以调用circleSpotter函数，找出它所在的奇数圈。下述代码中自oddcnt += 1始。

xxxxxxxxxx
12
1
for layer in layers:
2
    layerI = layers.index(layer)
3
    for x in range(len(layer)):
4
        i = layer[x]
5
        for j in layer[x+1:]:
6
            if array2[i][j] == 1: 
7
                innerLayer = True 
8
                oddcnt += 1
9
                oddCirs.append([i, j])
10
                oddCir = oddCirs[oddcnt]
11
                oddCir = circleSpotter(i, j, layerI, oddCir) 
12
                oddCirs[oddcnt] = oddCir

xxxxxxxxxx
4
1
>>> ★★层内有边，该网络不平衡。★★
2
>>> 构成奇数边数的圆的节点如下：
3
>>> [[0, 1, 2, 3, 4]]
4
>>> ★★★★该网络不是平衡网络。★★★★

<< 返回本书主页
<< Back to the afterword page