<< 返回本书主页
<< Back to the afterword page

2 同质性与社会网络的演化

吕汶桧 Wenhui Lyu

Jan. 2022

codes

2.1 背景问题

上一节的内容主要是对社会网络的一种静态考察，但现实社会网络总是处在演变之中。一个最为重要的演化现象是，一些原本互不认识的节点可能会在某一时间点结识，对应在网络中建立了一条新的边。

两个人的结识有一定规律可循，它受着“机会”、“信任”和“动机”的影响。当两个陌生人之间有中介（例如共同朋友）时，这一中介就会大大增加他们俩相遇的机会，也让他们更容易彼此信任，有时也会有让他们相互结识的动机。

两个节点经由共同朋友的中介结识，称为“三元闭包”（triadic closure）。课上，李老师给我们介绍了一个基于大数据的研究，它借助一所大学里的邮件往来信息，验证了三元闭包原理：两个互不认识的人，共同朋友越多，一段时间后他们结识的概率越高。

课上还提到，三元闭包原理的一个细化版本是“强三元闭包原理”。对于一个社会网络，我们把其中的边标识为两类，一类指示强关系，另一类指示弱关系。强三元闭包原理说的是，如果节点$i$$i$与节点$j$$j$有强关系，节点$i$$i$与节点$k$$k$也有强关系，那么，节点$j$$j$与节点$k$$k$之间至少应该有弱关系。

这里的分析还可以引入“捷径”（local bridge）概念，亦即其两端节点没有“共同朋友” 的边。基于“强三元闭包原理”，我们可以推导出“捷径→弱关系”定理：在标识了强弱关系的网络中，如果一个节点符合强三元闭包原理且有两个强关系朋友（设为$C$$C$和$D$$D$），则它与任何捷径相连的朋友（设为$A$$A$和$B$$B$）之间一定是弱关系。否则，$C$$C$或$D$$D$一定是$A$$A$和$B$$B$的共同朋友，$A$$A$和$B$$B$之间的边就不再是捷径。

社会网络演化的一个结果就是“同质性”：朋友（相近的人们）之间具有某种特征相似性，例如来自同一个地方。我们用“加入了某个‘社团’或‘俱乐部’”或“从事某件‘事’”，来刻画一个人的特征。当我们把“社团”概念考虑进社会网络以后，社会网络的演化不仅有“三元闭包”原理这一个规律，而且还有另外两个规律：

• “社团闭包”（social focal closure）原理：两个人经由共同社团结识，称为“社团闭包”。这种闭包里，“物以类聚，人以群分”，社会网络的同质性得以加强。
• “会员闭包”（membership closure）原理：社团闭包和三元闭包都讨论的是两个人之间新友谊的产生。除此以外，一个人在什么情况下会加入一个社团呢？与前两种闭包类似，当这个人已经有几个朋友参与了某一社团，ta有更多机会知晓、信任这一社团，更有动机加入它，总之是就更容易加入这个社团。这就是“会员闭包”。这种闭包里，“近朱者赤，近墨者黑”，社会网络的同质性得以加强。

2.2 计算实践：同质性作用下的网络演化过程

codes

2.2.1 作业描述与算法思路

本次作业的任务是，基于三个闭包原理，用编程来模拟社会网络的演化。

为了操作的方便，我们把三个闭包原理简化为三个门槛假设：

• 三元闭包：如果两个不相识的人有了s个或更多共同朋友，则他们下一时点前会成为朋友
• 社团闭包：如果两个不相识的人参加了f个或更多相同的俱乐部，则他们在下一时点前会成为朋友
• 会员闭包：如果某人有m个或更多朋友参加了某个俱乐部，则他在下一时点前参加该俱乐部

正如我们可以用邻接矩阵来表示一个社会网络中的朋友关系，我们还可以用一个归属矩阵来表示人对社交聚点（social focal）的归属关系。

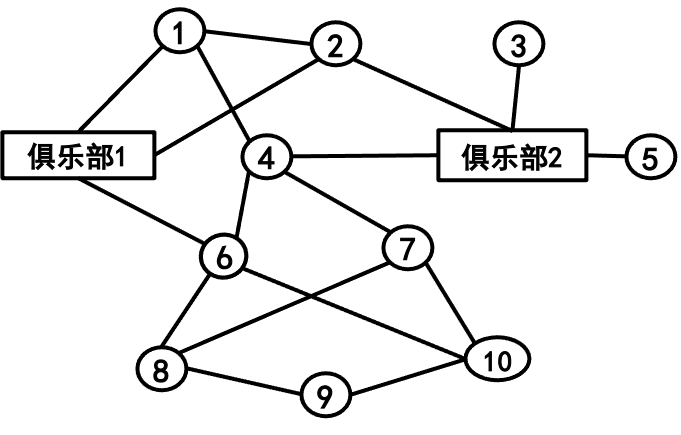
上面这个社会网络可以用下面两个矩阵表示：

• 邻接矩阵：表示人与人之间的朋友关系；

• 归属矩阵：表示人与社团之间的归属关系。例如，矩阵的第一行$\left(\begin{array}{cc}1& 0\end{array}\right)$$\begin{pmatrix}1 & 0\end{pmatrix}$表示，人$1$$1$加入了社团$1$$1$，但没有加入社团$2$$2$。

基于社会网络的矩阵化，三个闭包原理可以表示成如下的数学关系：

• 三元闭包：节点$i$$i$与节点$j$$j$建立一条边，当$A[i]\cdot A[j]\ge s$$A[i] \cdot A[j] \ge s$；
• 社团闭包：节点$i$$i$与节点$j$$j$建立一条边，当$B[i]\cdot B[j]\ge f$$B[i] \cdot B[j] \ge f$；
• 会员闭包：节点$i$$i$与社团$c$$c$建立一条边，当$A[i]\cdot B[][c]\ge m$$A[i] \cdot B[][c] \ge m$。

给定一个社会网络，我们考察它是否满足了上面三个临界条件，加上该加的边，生成下一轮的社会网络，我们再做同样的操作。如此循环，直到稳定，没有新边可加。

2.2.2 编程实现与要点说明

首先，我们还是需要调用读取数据文件的函数，把邻接矩阵和归属矩阵存储在两个numpy 2d-arrays里，前者是A，后者是B。s、f、m的值由用户指定。代码略，与1.2.1.2类似。输入值的一个例子如下：

xxxxxxxxxx
5
1
>>> 输入邻接矩阵文件名：./input/a.txt
2
>>> 输入归属矩阵文件名：./input/b.txt
3
>>> 请输入三元闭包的临界值（请输入整数）：3
4
>>> 请输入社团闭包的临界值（请输入整数）：2
5
>>> 请输入会员闭包的临界值（请输入整数）：2

接着，我写了检验闭包条件的函数edgeAdder，便于重复调用：输入两个矩阵的数据A、B和s、f、m的值，输出满足闭包条件、加上新边后的两个矩阵。

xxxxxxxxxx
1
1
def edgeAdder(A, B, an, bn, s, f, m):

三元闭包：一一检查网络中的边，当$A[i]\times A[j]\ge s$$A[i] \times A[j] \ge s$时，亦即np.dot(A[i], A[j]) >= s时，节点$i$$i$与节点$j$$j$建立一条边。这时我不应直接在邻接矩阵中作修改，否则会影响接下来对会员闭包的检验；我先把需要加的边存储在A_alters里。

xxxxxxxxxx
9
1
    A_alters = []
2
    B_alters = []
3
    for i in range(an):
4
        for j in range(i+1, an):
5
            if A[i][j] == 1:
6
                continue
7
            if np.dot(A[i], A[j]) >= s:
8
                A_alters.append([i, j])
9
                print('三元闭包（人，人）：\t%i %i' % (i, j))

社团闭包：当np.dot(B[i], B[j]) >= f时，节点$i$$i$与节点$j$$j$建立一条边，存储在A_alters里。

xxxxxxxxxx
7
1
    for i in range(an):
2
        for j in range(i+1, an):
3
            if A[i][j] == 1:
4
                continue
5
            if np.dot(B[i], B[j]) >= f:
6
                A_alters.append([i,j])
7
                print('社团闭包（人，人）：\t%i %i' % (i, j))

会员闭包：当np.dot(A[i], B[:,c]) >= m时，节点$i$$i$与社团$c$$c$建立一条边，存储在B_alters里。

xxxxxxxxxx
7
1
    for i in range(an):
2
        for c in range(bn):
3
            if B[i][c] == 1:
4
                continue
5
            if np.dot(A[i], B[:,c]) >= m:
6
                B_alters.append([i, c])
7
                print('会员闭包（人，事）：\t%i %i' % (i, c))

根据A_alters和B_alters的内容，统一对矩阵做出修改，加上该加的边。

xxxxxxxxxx
6
1
    for item in A_alters:
2
        A[item[0]][item[1]] = 1
3
        A[item[1]][item[0]] = 1
4
    for item in B_alters:
5
        B[item[0]][item[1]] = 1
6
    return A, B, len(A_alters) + len(B_alters)

主程序的内容，就是一轮接一轮地调用edgeAdder函数，加上该加的边，直到无边可加、演化结束。

xxxxxxxxxx
12
1
round = 1
2
print('第 1 轮：')
3
while True:
4
    A_new, B_new, alters = edgeAdder(A, B, An, Bn, s, f, m)
5
    if alters == 0:
6
        break
7
    else:
8
        A = A_new
9
        B = B_new
10
        round += 1
11
        print('第 %i 轮：' % round)
12
print('演化结束！')

15
1
>>> 第 1 轮：
2
>>> 三元闭包（人，人）：    5 6
3
>>> 三元闭包（人，人）：    7 9
4
>>> 会员闭包（人，事）：    0 1
5
>>> 会员闭包（人，事）：    3 0
6
>>> 第 2 轮：
7
>>> 社团闭包（人，人）：    1 3
8
>>> 会员闭包（人，事）：    6 0
9
>>> 第 3 轮：
10
>>> 会员闭包（人，事）：    7 0
11
>>> 会员闭包（人，事）：    9 0
12
>>> 第 4 轮：
13
>>> 会员闭包（人，事）：    8 0
14
>>> 第 5 轮：
15
>>> 演化结束！

<< 返回本书主页
<< Back to the afterword page