<< 返回本书主页
<< Back to the afterword page

10 表决：方式与挑战

codes

10.1 背景问题

在一个共同体里，人们观点相异极为常见。在异见的基础上决议或得出“集体意见”，表决是一种重要方式。

孔多塞原则与孔多塞悖论

表决有几种经典设计。一个代表是孔多塞原则：

• $m$$m$（奇数）个投票人，$n\ge 2$$n\geq2$个候选项；
• 每人给出对候选项的个人偏好全排序，作为自己的投票；
• 两两检查候选项，比较哪一候选项受到更多人偏好（少数服从多数的原则）；
• 给出候选项的全排序，作为集体结果。

这一过程可以用有向图来表示，下图是依据孔多塞原则表决的一个例子：

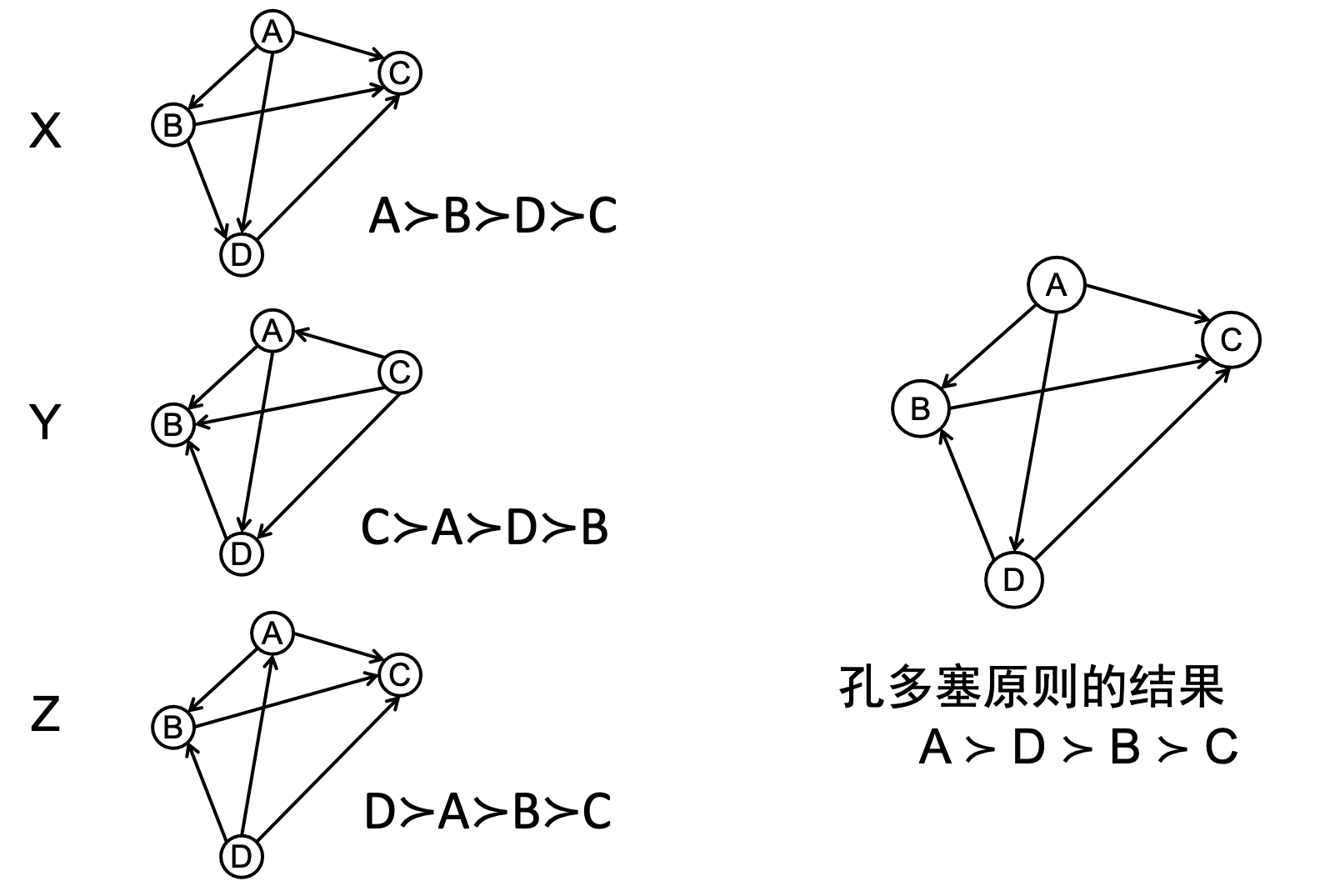
在集体全排序中，边$a\to b$$a\to b$意味着至少$(m+1)/2$$(m+1)/ 2$个个体偏好中有$a\to b$$a\to b$。如果投票人为奇数，任意两个节点之间有且仅有一条有向边。

这一表决原则的问题在于，可能会出现孔多塞悖论。假设三个人甲、乙、丙要对三个候选项A、B、C投票，

• 甲：$A\succ B\succ C$$A\succ B\succ C$，
• 乙：$B\succ C\succ A$$B\succ C\succ A$，
• 丙：$C\succ A\succ B$$C\succ A\succ B$。

最终的结果：$A\succ B,B\succ C,C\succ A$$A\succ B, B\succ C, C\succ A$，无法形成全排序，也说不清楚谁最被偏爱。这一悖论表明，即使个体理性、制度合理，也不一定能导致群体理性。

孔多塞悖论的解决

以下两种方法可以用来解决孔多塞悖论，保证找出胜者：

• 议程设置：按一定的议程顺序，每一轮分别对两个候选人投票，胜者进入下一轮。但是，如果存在孔多塞悖论，不同的议程设置会导致不同的胜者，但议程——这一无关变量——本不应该影响表决结果。
• 波达计数法：把每个人的全排序转换成给候选人的分数，排名越高的候选人分数越高。依此计算每一候选人的积分。但是，如果有的投票人使坏、采取策略性投票，仍然有可能出现有违公平的表决结果。例如，第二受欢迎的候选人B的投票者，为了把本来最受欢迎的A搞下去，可能把A排在最末；如果他们秉公投票，A在他们身上获得的分数并不应该如此低。一般性地讲，依照积分制比较A和B（$A\succ B⟺\sum (a_i-b_i)$$A \succ B \iff \sum (a_i-b_i)$），可能与“少数服从多数”的原则（$A\succ B⟺\sum sig(a_i-b_i)$$A \succ B \iff \sum sig(a_i-b_i)$）矛盾。

完美的表决方式似乎很难找到。阿罗在1950年提出了阿罗不可能定理：不存在同时满足以下三条公理的表决聚合规则，

• 非独裁：结果序不能等于某个参与人的个人序
• 一致性认同：如果大家都认为$A>B$$A>B$，结果中就应该是$A>B$$A>B$
• 独立于无关项：只要每个个体序中A和B的关系没变，结果中就不应该变

也就是说，任何一种表决规则至少违反以上三条公理之一。那么，是否存在对投票人的个人序做某种合理要求，能够克服阿罗不可能定理指出的困难呢？课堂上引入了一个新的标准——属性序——用以判断投票者是否足够理性，不理性的投票者的意见不予考虑。只考虑理性投票者似乎确实合理，这一方法也成功解决了孔多塞悖论。

在现实生活中，事物的性质往往能够按顺序排列，例如，候选项是建筑预算时，我们可以按照数额从大到小排列。对于这类事物，理性的投票行为应当符合单峰性质。例如，如果一个人对高、中、低三种建筑预算的排序是$\text{高}\text{预}\text{算}\succ \text{低}\text{预}\text{算}\succ \text{中}\text{预}\text{算}$$高预算\succ低预算\succ中预算$，这就违背了单峰性质，直观上也是不理性的选择：如果他最偏好高预算，得不到高预算时的次佳选项，应当是更接近首选的候选项，即中预算。

单峰偏好的定义如下：

• 假设候选项有一个属性序，$A_1\succ A_2\succ \dots \succ A_k\succ \dots \succ A_n$$A_1 \succ A_2 \succ \ldots \succ A_k \succ \ldots \succ A_n$。
• 给出的表决排序$A_k\succ \dots$$A_k \succ \ldots$（即$A_k$$A_k$排第一）满足单峰性质（单峰序），则对于所有$i<j<k$$i<j<k$和所有$i>j>k$$i>j>k$，$A_i$$A_i$排在$A_j$$A_j$的后面。

单峰性质可能呈现为以下三种形态。

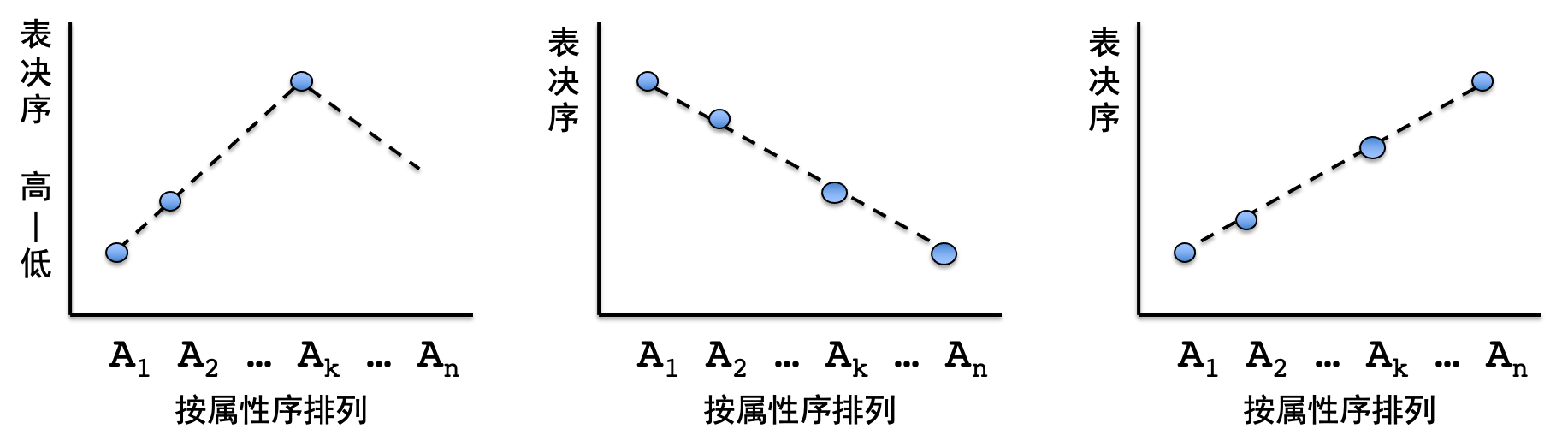
删去不理性的个体后，我们可以用中位项定理得出孔多塞全排序结果：给定满足单峰性质的$m$$m$个排序$R_1,R_2,\dots ,R_m$$R_1,R_2,\ldots,R_m$（$m$$m$是奇数）。若将所有人的全排序里的第一名$R_i(1)$$R_i(1)$按属性序$R_0$$R_0$排列，得到$S$$S$，则其中间项（$A_k$$A_k$）是孔多塞原则下的“胜者”。

这样操作的凭依就是排序的单峰性。设$S$$S$为$\dots ,A_t,\dots ,A_k,\dots ,A_s,\dots$$\ldots,A_t,\ldots,A_k,\ldots,A_s,\ldots$（中间项为$A_k$$A_k$）。

• 对于投票人$i$$i$，ta最偏好的候选项是$A_k$$A_k$或者任意一个属性序低于$A_k$$A_k$的候选项$A_t$$A_t$。由于个人全排序符合单峰性，ta一定觉得$A_k$$A_k$比任何一个属性序高于$A_k$$A_k$的候选项$A_s$$A_s$好。由于$A_k$$A_k$是中间项，投票人总数是奇数，这样想的人超过总数的一半。因此，超过一半的人认为$A_k\succ A_s$$A_k \succ A_s$。
• 同理，超过一半人偏好$A_k$$A_k$或者偏好一个属性序高于$A_k$$A_k$的候选项$A_s$$A_s$，他们一定认为$A_k$$A_k$比任何一个属性序低于$A_k$$A_k$的候选项$A_t$$A_t$好。

根据“少数服从多数”原则，中位项定理找出的$A_k$$A_k$一定是孔多塞胜者。

这样操作第一次，设孔多塞胜者为$A_{k1}$$A_{k1}$，它就是第一名。删去每个人全排序中的$A_{k1}$$A_{k1}$，单峰性质不变。用同样的方法，找出剩下的候选项中的孔多塞胜者$A_{k2}$$A_{k2}$，它就是第二名。迭代操作，最终获得整个集体排序。

10.2 计算实践：孔多塞模型下的表决综合

codes

10.2.1 作业描述与算法思路

本次作业就是模拟表决过程，给出表决结果。如果投票人的个人排序中不存在孔多塞悖论，就按照孔多塞原则确定群体排序；如果存在，就删去非理性投票者，按照中位项定理一个个确定胜者。

设有$m$$m$（奇数）个人参与对$n$$n$个项目（$p_1,p_2,\dots ,p_n$$p_1,p_2,\ldots,p_n$）的投票，每人提交一个对项目偏好的排序$R_1,R_2,\dots ,R_m$$R_1,R_2,\ldots,R_m$。你要做的事情是基于大家表达的偏好，尝试给出一个那些项目的群体排序$R$$R$，满足：若$p_i$$p_i$在$p_j$$p_j$前面，必须是$m$$m$个人中的多数认为$p_i$$p_i$应该在$p_j$$p_j$前面。我们知道，因为孔多塞悖论现象，基于个体偏好全序和多数原则综合的评判有可能形成不了一个体现群体意见的全序。你的任务是：

1. 如果$R_1,R_2,\dots ,R_m$$R_1,R_2,\ldots,R_m$之中没有隐含孔多塞悖论，则按照孔多塞原则给出体现群体意见的全序$R$$R$。

2. 如果有悖论：

   • 假设（$p_1,p_2,\dots ,p_n$$p_1,p_2,\ldots,p_n$）是人们关心的$n$$n$个项目的一种属性序，判断$R_1,R_2,\dots ,R_m$$R_1,R_2,\ldots,R_m$之中有哪些不满足单峰偏好性质，认为它们不是一个“理性投票”，将它们剔除。
   • 剩下的$k$$k$个若不是奇数，则以（$p_1,p_2,\dots ,p_n$$p_1,p_2,\ldots,p_n$）为附加个体序，凑成$k+1$$k+1$（奇数）。
   • 按中位项定理的操作方法给出全序$R$$R$。

这一算法有三个重点：

• 孔多塞悖论的判定标准：关键在于结果序中是否存在有向环。如果存在有向环，这一表决就有孔多塞悖论。根据第九讲里有向图的性质，如果一个有穷有向图中不存在有向环，则该图中既存在出度为0的节点，也存在入度为0的节点。尝试不断删除入度为0的节点。当且仅当找不到入度为0的节点、但还没有删除完所有节点，该图就存在有向环。

• 孔多塞排序：

  • 李老师提供的算法：和上述操作类似，在孔多塞有向图结果中不断删除入度为0的节点（入度为0意味着比所有其他候选项都更受偏好），如果一直可以删除到最后，则删除的顺序就是集体排序。
  • 我的算法：冒泡排序。一开始设定第一个候选项是第一名，排序列表里只有一个元素。依次考虑剩下的候选项。对于未加入排名的候选项$i$$i$，从队末开始，比较$i$$i$和序列中的元素，直到找到比$i$$i$更受偏爱的元素$j$$j$，把$i$$i$插入到$j$$j$后面。

• 检查个体偏好序是否符合单峰性质：找出投票人最为偏好的候选项$A_k$$A_k$。对于属性序低于$A_k$$A_k$所有的候选项，偏好序应当关于属性序单减；对于属性序高于$A_k$$A_k$所有的候选项，偏好序应当关于属性序单增。

10.2.2 编程实现与要点说明

首先，打开用户指定的数据文件，读取所有投票者的投票结果，存储在一个numpy 2d-array votes里。代码略，参见1.2.1.2。一个数据文件的例子如下：

xxxxxxxxxx
15
1
>>> 输入文件名：b4
2
>>> 投票结果：
3
>>> [[9 8 7 6 5 4 3 2 1 0]
4
>>>  [2 3 1 4 5 6 0 7 8 9]
5
>>>  [7 6 5 8 4 3 2 1 0 9]
6
>>>  [3 4 2 5 6 1 7 0 8 9]
7
>>>  [6 7 5 4 3 2 1 8 0 9]
8
>>>  [2 1 3 0 4 5 6 7 8 9]
9
>>>  [0 1 2 3 4 5 6 7 8 9]
10
>>>  [3 4 5 2 1 6 7 0 8 9]
11
>>>  [3 0 9 7 6 8 1 5 4 2]
12
>>>  [9 7 5 8 1 3 2 0 4 6]
13
>>>  [3 6 1 7 2 9 8 0 4 5]
14
>>>  [2 9 0 6 8 3 1 5 7 4]
15
>>>  [8 7 1 2 3 4 9 6 5 0]]

定义一个函数compare，用以比较两个候选项中哪个候选项得到了多数人的支持。advantage大于0，i比j得到了更多人支持。

xxxxxxxxxx
13
1
def compare(i,j,votes): 
2
    n = len(votes) # number of voters
3
    advantage = 0 # accumulative advantage of i over j according to all voters
4
    i_indices = np.where(votes == i)
5
    j_indices = np.where(votes == j)
6
    for k in range(n):
7
        i_index = i_indices[1][k]
8
        j_index = j_indices[1][k]
9
        if i_index < j_index: # i ranks higher than j, according to voter k
10
            advantage += 1
11
        else:
12
            advantage -= 1
13
    return advantage

定义函数condorcet，根据孔多塞定理，得到集体序order。

xxxxxxxxxx
5
1
def condorcet(votes):
2
    n = len(votes) # number of voters
3
    assert n % 2 == 1 # make sure there are an odd number of voters
4
    m = len(votes[0]) # number of candidates
5
    order = [0]

我这里使用的是冒泡排序法。对于尚未加入集体序的元素i，把它同该序列中的元素一一比较大小，从最后一名开始比。直到找到比i更受欢迎的元素j，把i插在j后面。

xxxxxxxxxx
9
1
    for i in range(1, m):
2
        for j_index in range(len(order)):
3
            flag = False
4
            j = order[len(order) - j_index - 1]
5
            advantage = compare(i, j, votes)
6
            if advantage < 0:
7
                order.insert(j_index+1, i)
8
                flag = True
9
                break

如果没有找到比i更受欢迎的元素j，这意味着i是目前为止得票最多的候选项，把它放在第一位。

xxxxxxxxxx
3
1
        if flag == False:
2
            order.insert(0, i)
3
    return order

定义函数condorcet_paradox_check，检查投票结果是否隐含孔多塞悖论。这一函数的内部结构略微有些复杂，我定义了两个局部函数：preference_matrix_generator、most_preferred_deleter。在函数condorcet_paradox_check内部的主程序中，我先调用preference_matrix_generator，生成孔多塞有向图，在对这一有向图迭代调用most_preferred_deleter，不断删除入度为0的节点，来判断孔多塞悖论是否存在。

xxxxxxxxxx
3
1
def condorcet_paradox_check(votes):
2
    m = len(votes[0])
3
    n = len(votes)

函数preference_matrix_generator根据投票结果votes生成孔多塞排序有向图preference_matrix，这一过程主要依靠迭代调用compare函数完成。preference_matrix[i][j] = 1表示$i\to j$$i \to j$，preference_matrix[i][j] = -1表示$j\to i$$j \to i$。

xxxxxxxxxx
16
1
    def preference_matrix_generator(votes): 
2
        preference_matrix = np.zeros((m,m))
3
        assert n % 2 == 1
4
        for i in range(m-1):
5
            for j in range(i+1,m):
6
                advantage = compare(i, j, votes)
7
                if advantage > 0: # i is more preferred than j
8
                    preference_matrix[i][j] = 1
9
                    preference_matrix[j][i] = -1
10
                else:
11
                    preference_matrix[i][j] = -1
12
                    preference_matrix[j][i] = 1
13
        return preference_matrix
14
    preference_matrix = preference_matrix_generator(votes)
15
    print('孔多塞排序有向图（初始）：')
16
    print(preference_matrix)

xxxxxxxxxx
11
1
>>> 孔多塞排序有向图（初始）：
2
>>> [[ 0. -1. -1. -1. -1. -1. -1. -1.  1.  1.]
3
>>>  [ 1.  0. -1. -1.  1.  1. -1.  1.  1.  1.]
4
>>>  [ 1.  1.  0. -1.  1.  1.  1. -1.  1.  1.]
5
>>>  [ 1.  1.  1.  0.  1.  1.  1.  1.  1.  1.]
6
>>>  [ 1. -1. -1. -1.  0.  1.  1. -1. -1.  1.]
7
>>>  [ 1. -1. -1. -1. -1.  0. -1. -1.  1.  1.]
8
>>>  [ 1.  1. -1. -1. -1.  1.  0.  1.  1.  1.]
9
>>>  [ 1. -1.  1. -1.  1.  1. -1.  0.  1.  1.]
10
>>>  [-1. -1. -1. -1.  1. -1. -1. -1.  0.  1.]
11
>>>  [-1. -1. -1. -1. -1. -1. -1. -1. -1.  0.]]

接下来的任务是判断这一有向图是否存在有向环。函数most_preferred_deleter用以检查有向图中是否存在入度为0的点，如果存在，就删除它。返回该有向图是否存在入度为0的点的bool值deleter_bool，和删除入度为0的点后的有向图preference_matrix。

xxxxxxxxxx
15
1
    def most_preferred_deleter(preference_matrix):
2
        deleter_bool = False # whether there is indeed a node to be deleted
3
        for i in range(len(preference_matrix)):
4
            preference_individual = preference_matrix[i]
5
            flag = True
6
            for item in preference_individual:
7
                if item < 0:
8
                    flag = False
9
                    break
10
            if flag == True:
11
                deleter_bool = True
12
                preference_matrix = np.delete(preference_matrix, i, 0)
13
                preference_matrix = np.delete(preference_matrix, i, 1)
14
                break # There's no possibility that a given matrix has two nodes whose entry degrees are 0 at the same time
15
        return preference_matrix, deleter_bool

循环调用most_preferred_deleter函数，直到无节点可删。此时，如果所有节点都删除掉了，有向图中不存在环，孔多塞悖论不存在；反之则存在孔多塞悖论。

xxxxxxxxxx
12
1
    while True:
2
        preference_matrix, deleter_bool = most_preferred_deleter(preference_matrix)
3
        # print(preference_matrix)
4
        if deleter_bool == False: 
5
            break # break when there is no node to be deleted
6
    if len(preference_matrix) == 0:
7
        paradox_bool = False
8
        print('不存在孔多塞悖论。')
9
    else:
10
        paradox_bool = True
11
        print('存在孔多塞悖论。')
12
    return paradox_bool

如果孔多塞悖论存在，我们需要检查个体序是否符合单峰性质，删除非理性的投票者。我的程序中完成这一任务的是函数irrational_voters_deleter。我定义了两个局部函数monotonic_check和single_peak_check，后者需要调用前者。在irrational_voters_deleter的主程序中，我一一检查每个节点，调用single_peak_check，检查它们是否具有单峰性，删除不具有单峰性的节点。

xxxxxxxxxx
1
1
def irrational_voters_deleter(votes):

先定义一个函数monotonic_check，检查字典的值value是否随着键key单调变化。输入：

• order_dict变量：值是某一候选项的属性位次，键是它的个体偏好位次；
• right_or_left（字符串）：order_dict里的候选项在单峰的左侧还是右侧。

单峰左侧的候选项，偏好位次随着属性位次单减，返回mononotic_bool=True，否则返回mononotic_bool=False；单峰右侧的候选项，偏好位次随着属性位次单增，返回mononotic_bool=True，否则返回mononotic_bool=False。

xxxxxxxxxx
3
1
    def monotonic_check(order_dict, right_or_left): 
2
        # order_dict -- candidate : order
3
        monotonic_bool = True

首先把字典的键和值分别按照从小到大排序，得到keys和values。

xxxxxxxxxx
4
1
        keys = list(order_dict.keys())
2
        keys.sort()
3
        values = list(order_dict.values())
4
        values.sort()

考虑处于keys第i位的key。如果单调递增，处于values第i位value应当恰好等于order_dict[key]；如果单调递减，处于values从队末开始数第i位（从队首开始数第values_len - i - 1）的value应当恰好等于order_dict[key]。

xxxxxxxxxx
13
1
        for i in range(len(keys)):
2
            key = keys[i]
3
            values_len = len(values)
4
            if right_or_left == 'right': 
5
                value = values[i]
6
            elif right_or_left == 'left': 
7
                value = values[values_len - i - 1]
8
            else:
9
                raise Exception('The argument “right_or_left” for function *monotonic_check* need a string variable which is either "right" or "left".')
10
            if order_dict[key] != value: 
11
                monotonic_bool = False
12
                break
13
        return monotonic_bool

在检查单峰性的函数single_peak_check中，我们只需要确定最受偏好的候选项most_preferred，把它左侧的候选项存入字典leftwing中，右侧的候选项存入rightwing中，再分别调用monotonic_check即可。返回rightwing_bool and leftwing_bool：左右候选项同时通过单调测试，这一投票者的偏好序就具有单峰性。

xxxxxxxxxx
14
1
    def single_peak_check(votes_individual): 
2
        most_preferred = votes_individual[0]
3
        rightwing = {} # votes on those candidates whose attributive order is higher than the most preferred one
4
        leftwing = {} # votes on those candidates whose attributive order is lower than the most preferred one
5
        for i in range(most_preferred + 1, m):
6
            i_index = np.where(votes_individual == i)
7
            rightwing[i] = i_index[0][0]
8
        for i in range(0, most_preferred):
9
            i_index = np.where(votes_individual == i)
10
            leftwing[i] = i_index[0][0]
11
        # The voter's behavior satisfies single-peak attribute, when both the left wing and the right wing are monotonic
12
        rightwing_bool = monotonic_check(rightwing, 'right')
13
        leftwing_bool = monotonic_check(leftwing, 'left')
14
        return rightwing_bool and leftwing_bool

一一检查有向图中的节点，输出不理性的投票者。

xxxxxxxxxx
9
1
    m = len(votes[0])
2
    irrational_voters = []
3
    for i in range(len(votes)):
4
        votes_individual = votes[i]
5
        single_peak_bool = single_peak_check(votes_individual)
6
        if single_peak_bool == False:
7
            irrational_voters.append(i)
8
    print('违反单峰性质的voters序号（初始矩阵行号）：', end = '')
9
    print(irrational_voters)

xxxxxxxxxx
1
1
>>> 违反单峰性质的voters序号（初始矩阵行号）：[8, 9, 10, 11, 12]

删除非理性投票者，生成新的有向图矩阵。

xxxxxxxxxx
14
1
    ## generate a new matrix which excludes the irrational voters
2
    n = len(votes)
3
    cnt = 0
4
    for i in range(n):
5
        if i in irrational_voters:
6
            continue
7
        if cnt == 0:
8
            votes_new = votes[i]
9
            votes_new = np.reshape(votes_new, (-1, m)) # 1d to 2d (in order to concatenate into a 2-d array)
10
        else:
11
            votes_appended = votes[i]
12
            votes_appended = np.reshape(votes_appended, (-1, m))
13
            votes_new = np.concatenate((votes_new, votes_appended), axis = 0)
14
        cnt += 1

检查投票者是否为奇数个。如果不是，补齐一个一个投票者，其偏好序为属性序。

xxxxxxxxxx
8
1
    if len(votes_new) % 2 == 0:
2
        print('删除非理性投票者后，总人数不为奇数，补齐一个投票者，其偏好序为属性序。')
3
        votes_default = np.array([[0,1,2,3,4,5,6,7,8,9]])
4
        votes_new = np.concatenate((votes_new, votes_default), axis = 0)
5
    print('删除非理性投票者后的矩阵为：')
6
    print(votes_new)
7
    
8
    return votes_new

xxxxxxxxxx
11
1
删除非理性投票者后，总人数不为奇数，补齐一个投票者，其偏好序为属性序。
2
删除非理性投票者后的矩阵为：
3
[[9 8 7 6 5 4 3 2 1 0]
4
 [2 3 1 4 5 6 0 7 8 9]
5
 [7 6 5 8 4 3 2 1 0 9]
6
 [3 4 2 5 6 1 7 0 8 9]
7
 [6 7 5 4 3 2 1 8 0 9]
8
 [2 1 3 0 4 5 6 7 8 9]
9
 [0 1 2 3 4 5 6 7 8 9]
10
 [3 4 5 2 1 6 7 0 8 9]
11
 [0 1 2 3 4 5 6 7 8 9]]

对于理性投票者集合，我们采用中位项定理排序。先定义函数median_identifier，给定一组投票结果votes，集合每一投票者最偏好的候选项most_preferred_choices，找出其中的中位项i，这就是当前votes中的孔多塞胜者。

xxxxxxxxxx
6
1
def median_identifier(votes):
2
    candidates_num = len(votes[0])
3
    n = len(votes)
4
    most_preferred_choices = [] 
5
    for votes_individual in votes:
6
        most_preferred_choices.append(votes_individual[0])

为了找出中位项，我调用了numpy的unique方法，得到一个字典occurences，其中记录了每一候选项成为最受偏好者的次数（被多少人选为了最佳）。

xxxxxxxxxx
3
1
    most_preferred_choices_array = np.array(most_preferred_choices)
2
    unique, counts = np.unique(most_preferred_choices_array, return_counts=True)
3
    occurences = dict(zip(unique, counts))

occurences的键按照属性序从小到大排列，加总每一候选项的出现次数，总和存储在变量accumulation里。当accumulation >= (n+1) // 2时，终止循环，此时的candidate即为中间项。

xxxxxxxxxx
7
1
    accumulation = 0
2
    for candidate in occurences.keys():
3
        accumulation += occurences[candidate]
4
        if accumulation >= (n+1) // 2:
5
            break
6
    print(candidate, end = ', ')
7
    return candidate

以下为主程序。

首先调用condorcet_paradox_check，检查投票结果是否存在孔多塞悖论。

xxxxxxxxxx
1
1
paradox_bool = condorcet_paradox_check(votes)

如果不存在孔多塞悖论，就调用condorcet，按照孔多塞原则排序。

xxxxxxxxxx
4
1
if paradox_bool == False:
2
    condorcet_order = condorcet(votes)
3
    print('根据孔多塞定理，全排序如下：', end = '')
4
    print(condorcet_order)

否则就调用irrational_voters_deleter，删除非理性投票者，得到votes_new。

xxxxxxxxxx
3
1
else:
2
    votes_new = irrational_voters_deleter(votes)
3
    rational_voters_num = len(votes_new)

接着调用median_identifier，按照中位项定理确定当前的孔多塞胜者median_choice，然后在投票结果votes_new中删去这一候选项。迭代操作，直到所有候选项都被排到集体序中。

xxxxxxxxxx
8
1
    print('根据中位项定理，全排序如下：', end = '')
2
    while True:
3
        median_choice = median_identifier(votes_new)
4
        if len(votes_new[0]) == 1:
5
            break
6
        m = len(votes_new[0]) - 1
7
        votes_new = votes_new[votes_new != median_choice]
8
        votes_new = np.reshape(votes_new, (rational_voters_num, m))

xxxxxxxxxx
1
1
>>> 根据中位项定理，全排序如下：3, 4, 2, 5, 1, 6, 7, 0, 8, 9,

上面的数据例子存在孔多塞悖论。以下是一个不存在孔多塞悖论的数据例子：

xxxxxxxxxx
17
1
>>> 输入文件名：b2
2
>>> 投票结果：
3
>>> [[4 3 2 1 0]
4
>>>  [3 2 1 0 4]
5
>>>  [1 0 2 3 4]
6
>>>  [4 1 0 3 2]
7
>>>  [1 3 2 0 4]
8
>>>  [4 2 3 1 0]
9
>>>  [4 2 0 3 1]]
10
>>> 孔多塞排序有向图（初始）：
11
>>> [[ 0. -1. -1. -1. -1.]
12
>>>  [ 1.  0. -1. -1. -1.]
13
>>>  [ 1.  1.  0. -1. -1.]
14
>>>  [ 1.  1.  1.  0. -1.]
15
>>>  [ 1.  1.  1.  1.  0.]]
16
>>> 不存在孔多塞悖论。
17
>>> 根据孔多塞定理，全排序如下：[4, 3, 2, 1, 0]

<< 返回本书主页
<< Back to the afterword page